УДК 681
АВТОМАТИКА И
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
1979, №5,
стр. 33-40
____________________________________________
УДК 681.326.06
В. Ф. Звягин, В. Н. Голыничев, О, Ф.
Немолочнов
МЕТОД СИНТЕЗА КОРРЕКТНЫХ
ПОСЛЕДОВАТЕЛЬНОСТЕЙ ДЛЯ ЛОГИЧЕСКИХ СХЕМ
Будем рассматривать комбинационные и
последовательностные асинхронные схемы,
построенные из логических элементов И, ИЛИ, И—НЕ,
ИЛИ—НЕ. Описанием схемы служит схемный список, в
котором заданы типы элементов и структура связей
между ними. Корректными последовательностями
для асинхронных логических схем считаются
последовательности, свободные от критических
состязаний сигналов и генерации. В работе
рассматриваются логические схемы, корректное
функционирование которых не основывается на
соотношении задержек в схеме. Основное внимание
уделено вопросу синтеза корректных
последовательностей для асинхронных схем с
памятью. Особенностью предлагаемого метода
является то, что синтезированные
последовательности корректны по построению и не
требуют последующего анализа по методике
троичного моделирования. В работе описывается
принятая модель логической схемы, вводятся в
рассмотрение обобщенные кубические покрытия,
предлагается модель переключения схемы,
формулируется и доказывается критерий
корректности перехода.
1.Модель схемы. Принята
модель основывается на применении аппарата
исчисления кубических комплексов [1].
Переключательная функция, реализуемая схемой,
отображается кубическими покрытиями С(z0=0)
и С(z0=1), позволяющими в компактной
векторной форме задать все множество входных
воздействий, требующихся для получения искомого
логического значения z0 на выходе схемы.
Каждой координате куба покрытия поставлен в
соответствие вход схемы. Формат покрытия С(z0)
есть упорядоченный список входов,
сопоставленный координатам покрытия С(z0).
Каждая координата куба c из С(z0) может
принимать логическое значение из множества {0, 1,
x}, где под x понимается значение, не
используемое в данном кубе для получения z0
. Понятие кубического покрытия С(z0)
можно распространить на последовательностные и
многовыходные схемы.
Комбинационные схемы.
Покрытие С(z0) дл одновыходной
схемы может быть построено по 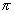 * -алгоритму [1, 2]. В случае
многовыходной схемы состояние выходов будем
описывать вектором логических значений Z0=(z01,z02,…,z0n),
где п -- число выходов. Всего возможно 3n
-1 комбинаций Z0,Z0
* -алгоритму [1, 2]. В случае
многовыходной схемы состояние выходов будем
описывать вектором логических значений Z0=(z01,z02,…,z0n),
где п -- число выходов. Всего возможно 3n
-1 комбинаций Z0,Z0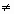 (хх ... х); соответственно может
быть построено 3n —1 покрытий С(Z0). Координаты
вектора Z0 принимают значения из множества
{0, 1, х}. Куб
(хх ... х); соответственно может
быть построено 3n —1 покрытий С(Z0). Координаты
вектора Z0 принимают значения из множества
{0, 1, х}. Куб 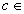 С(Z0)
задается в виде ХZ', где X - вектор входных
логических значений. Z’=Z’(X) - вектор выходных
логических значений, Z’Z0. Покрытие С(Z0)
может быть получено путем подстановки и
пересечения кубов покрытий С(z0k),
С(Z0)
задается в виде ХZ', где X - вектор входных
логических значений. Z’=Z’(X) - вектор выходных
логических значений, Z’Z0. Покрытие С(Z0)
может быть получено путем подстановки и
пересечения кубов покрытий С(z0k),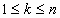 , X и Z' называются
в дальнейшем подкубами куба ХZ'.
, X и Z' называются
в дальнейшем подкубами куба ХZ'.
Последовательностные схемы.
Простейшая последовательностна схема
соответствует элементу памяти. Текущее
состояние у' элемента памяти определяется
значением входов X и y - состоянием
элемента памяти в предыдущий момент времени, у'
= у'(Х, у). Покрытие С (y0) можно построить по  *-алгоритму, добавив
псевдовход у в формат покрытия. Кубы покрыти С
(уа) записываются в формате Хуу'. Покрытие
С (y0) подразделяется на две области: C(y0)
= Cx(y0)
*-алгоритму, добавив
псевдовход у в формат покрытия. Кубы покрыти С
(уа) записываются в формате Хуу'. Покрытие
С (y0) подразделяется на две области: C(y0)
= Cx(y0)  Cp(y0),
y0=p, p
Cp(y0),
y0=p, p {0, 1}.
{0, 1}.
Кубы из области Сх соответствуют
установке схемы в текущее состояние у' = р независимо
от предыдущего состояния y. В наборе,
соответствующем c Cx(y0),
все петли обратной связи элемента памяти
разомкнуты. Набором считается любое двоичное
доопределение куба с.
Cx(y0),
все петли обратной связи элемента памяти
разомкнуты. Набором считается любое двоичное
доопределение куба с.
Кубы из области Ср соответствуют
хранению значения у' = у = р. В наборе,
соответствующем с Сp(y0),
замкнута петля обратной связи элемента памяти.
В работе [3] исследовались свойства покрытия С(у0),
там же было показано, что
Сp(y0),
замкнута петля обратной связи элемента памяти.
В работе [3] исследовались свойства покрытия С(у0),
там же было показано, что  *-алгоритм сохраняет информацию о
состзательных свойствах схемы. Куб c
*-алгоритм сохраняет информацию о
состзательных свойствах схемы. Куб c C(Y0) для
многовыходной последовательностной схемы имеет
вид с=ХУУ'. В данном случае X - вектор
логических значений на входах схемы, У-
вектор логических значений на выходах элементов
памяти в предыдущий момент времени, У'=- У' (Х, У) -
вектор логических значений на выходах элементов
памяти в текущий момент времени, X, У, У' - подкубы
куба с
C(Y0) для
многовыходной последовательностной схемы имеет
вид с=ХУУ'. В данном случае X - вектор
логических значений на входах схемы, У-
вектор логических значений на выходах элементов
памяти в предыдущий момент времени, У'=- У' (Х, У) -
вектор логических значений на выходах элементов
памяти в текущий момент времени, X, У, У' - подкубы
куба с С(Y0).
Покрытие С (Y0) можно подразделить на две
области:
С(Y0).
Покрытие С (Y0) можно подразделить на две
области:
С(Yо) = Сx(Y0)  СР(Yо).
СР(Yо).
Области Сp соответствует У'=У.
Кубы из Ср обеспечивают хранение
состояния У', на графе переходов [4] такие кубы
сопоставляются петлям при вершине У'. При
подаче на схему набора, соответствующего кубу c Cp(Y0), c =
ХУ'У', замкнуты петли обратной связи элементов
памяти у'0k
Cp(Y0), c =
ХУ'У', замкнуты петли обратной связи элементов
памяти у'0k x
. Области Сх соответствует У'
x
. Области Сх соответствует У' У. Это означает, что
кубы из Сх обеспечивают выработку
состояния У' при условии хранени состояния У;
на графе переходов такие кубы сопоставляются
дугам, направленным из У в У' . При У=(хх...х)
куб c
У. Это означает, что
кубы из Сх обеспечивают выработку
состояния У' при условии хранени состояния У;
на графе переходов такие кубы сопоставляются
дугам, направленным из У в У' . При У=(хх...х)
куб c Cx(Y0)
обеспечивает начальную установку схемы. Дл
корректного переключения, соответствующего кубу
c
Cx(Y0)
обеспечивает начальную установку схемы. Дл
корректного переключения, соответствующего кубу
c Cx(Y0), на
схему действуют одновременно две составляющие X*
и X:
Cx(Y0), на
схему действуют одновременно две составляющие X*
и X:
- с = Х*У У', c=Cx(Y0) куб с - обеспечивает
установку элементов памяти.
- d=СР(У0), d = ХУУ.
Куб d обеспечивает
корректное сохранение состояния Y
Таким образом, У'=У У*, где У*— вектор значений
элементов памяти, устанавливающихся под
воздействием входов X* при условии хранения
значений элементов памяти из Y. Элементы памяти
из У' разбиваются на две области:
У*, где У*— вектор значений
элементов памяти, устанавливающихся под
воздействием входов X* при условии хранения
значений элементов памяти из Y. Элементы памяти
из У' разбиваются на две области:
- В области Y замкнуты петли обратной связи
элементов памяти и глобальные обратные связи.
Область Y замкнута и не использует значений из У*
- В области У* все петли обратной связи
разомкнуты. Для установки элементов памяти из У*
используются значения из области Y
В эвристическом алгоритме синтеза,
предложенном в [5], не накладывается ограничений
на взаимосвязь элементов памяти, и это приводит к
получению некорректных наборов и переходов. В
предлагаемом методе синтеза производится
динамический выбор ациклической области У* и замкнутой
области Y отдельно для каждого набора. Теоремы,
приведенные ниже, обосновывают этот выбор и
позволяют избавиться от некорректных
последовательностей, характерных дл итеративных
комбинационных схем [5].
В принятой модели информация о схеме
хранится в виде кубических покрытий элементов
памяти С(у0) и кубических покрытий
одновыходных комбинационных подсхем С (Z0).
С помощью ориентированного графа задается
структура соединения подсхем. Выбор подсхем
достаточно произволен, важно лишь, чтобы в
подсхему, соответствующую элементу памяти,
попала петля (или петли) обратной связи этого
элемента памяти. Размер подсхем выбирается в
соответствии с машинными ограничениями на число
координат в формате покрытия и ограничениями на
число кубов в покрытии. Куб с С(Y0) может быть получен из
покрытий С (z0), С (y0) по методу простых
кубов, предложенному в работе [6].
С(Y0) может быть получен из
покрытий С (z0), С (y0) по методу простых
кубов, предложенному в работе [6].
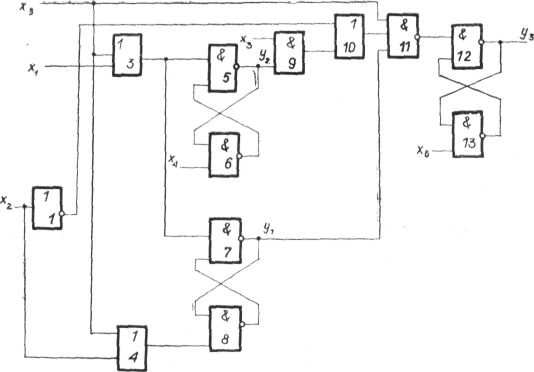
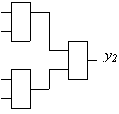
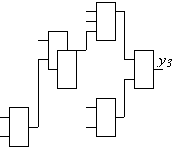
Рис. 1. Логическая схема. Выходы
элементов памяти y1,y2,y3.
Пример представлени
последовательностной схемы (рис. 1) приведен в
таблице. Схема содержит 3 элемента памяти и
поэтому состоит из трех подсхем. Области Сх(у0)
и Сp(у0) в таблице разделены
горизонтальной чертой.
Подсхемы |
Кубические
покрытия |
единичное 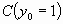 |
нулевое 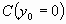 |
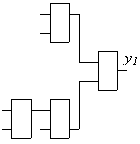
|
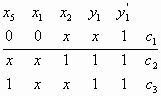
|
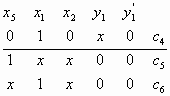
|
|
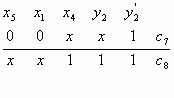
|
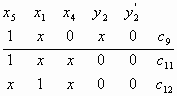
|
|
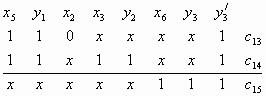
|
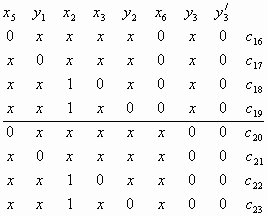
|
2. Свойства кубических покрытий. В
данном разделе рассматриваются свойства
кубических покрытий и условия корректности
переходов по покрытиям С(z0), С(Z0),
С(y0) и С(У0). Входной вектор X может
принимать 3m-1 значений, где m- число входов
схемы. В реальном эксперименте на схему может
подаваться произвольное двоичное доопределение
вектора X. Координаты у'k=p в кубе с =
ХУУ' при любом двоичном доопределении X вырабатываются
корректно. Это будет показано в дальнейшем.
Переход от набора А к набору В будет
корректным для комбинационной схемы, если
логическое значение z(В)=p выработано без
риска сбоя. Определим условия корректности через
троичную функцию. В терминах троичного
пространства (0,1,x) удается сформулировать
условия корректности поведения схемы в
пространстве (0,1). Введем в рассмотрение три
кубических комплекса:
Определим троичную функцию g(A)=.z*(A)
троичного аргумента A следующим образом
- g(A)=0, если A
 N0
N0
- g(A)=1, если A
 N1
N1
- x, если A
 Nx
Nx
Основным свойством троичной функции
явлется монотонность, из А В следует, что g(А)
В следует, что g(А) g(В). Доказательство монотонности,
как и доказательство всех последующих
утверждений, вынесено в приложение. Определим
векторную покоординатную операцию D = А/В следующим
образом:
g(В). Доказательство монотонности,
как и доказательство всех последующих
утверждений, вынесено в приложение. Определим
векторную покоординатную операцию D = А/В следующим
образом:
- dk, если ak=bk
- иначе dk= x
Операция А/В в геометрической
интерпретации соответствует поиску куба D наименьшей
размерности, содержащего кубы А и В. Операцию
D = А/В назовем операцией вычислени
переходного вектора D. В результате
выполнения этой операции будут найдены
координаты, постоянные на переходе от набора А к
набору В. Взаимосвязь троичной функции g(A) и
двоичной функции, реализуемой схемой и заданной
в виде покрытий С(z0 = 0) и С(z0=1),
описывается следующей теоремой.
Теорема 1. Выход схемы, заданной
покрытиями С(z0 = 0) и С(z0=1), может
измениться при переходе от набора А к набору В
тогда и только тогда, когда g(A/В)=х.
Условие появления статического риска
сбоя в терминах троичной функции можно
сформулировать в виде следующей теоремы.
Теорема 2. Статический риск сбоя на
выходе схемы может появиться на переходе от
набора А к набору В тогда и только тогда,
когда g(A/В)=x.
Критерий отсутствия статического
риска сбоя можно записать в нескольких
эквивалентных формах, являющихся следствиями
теоремы 2.
- g(А/В)=p, z(А)=z(В)=р.
- A/B
 c, с
c, с С(z0 = р), z(A)=z(В) =p.
С(z0 = р), z(A)=z(В) =p.
- g(А/В)=g(А)/g(В),
g(A)=g(B)=p.
Если A B, то
говорят, что A является гранью В, а В когранью
A. Переход с грани A на ее когрань В и наоборот
происходит без статического риска сбоя.
B, то
говорят, что A является гранью В, а В когранью
A. Переход с грани A на ее когрань В и наоборот
происходит без статического риска сбоя.
Нетрудно убедиться в том, что критерий
отсутствия статического риска сбоя остается
справедливым и для многовыходных схем Z*(А/В)
=Z*(А)/Z*(В).
Для простейшей последовательностной
схемы переходы с постоянным значением p задаются
кубами из области СР(y0 = р). Критерий
отсутствия статического риска сбоя записывается
как A/B c,c
c,c Cp(y0=p). В
работе [3] показано, что критерий отсутствия
критических состязаний сигналов имеет следующий
вид: z(А)=p, z(В)=р, В
Cp(y0=p). В
работе [3] показано, что критерий отсутствия
критических состязаний сигналов имеет следующий
вид: z(А)=p, z(В)=р, В d,d
d,d Cx(у0 = р). В
том случае, когда В
Cx(у0 = р). В
том случае, когда В d,d
d,d Сх(у0 = р), элемент
памяти работает в режиме установки, а это
означает, что петли обратной связи разомкнуты.
Сх(у0 = р), элемент
памяти работает в режиме установки, а это
означает, что петли обратной связи разомкнуты.
Критерий корректности переключени
схемы.
Переключением схемы с несколькими
элементами памяти назовем переход из состояния У'i-1
в состояние У'i такой, что У'i-1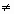 У'i. Будем
считать переход корректным, если он свободен от
генерации, критических состязаний сигналов и
риска сбоя. Обычно граф корректного перехода
описывается следующим образом: У'i-1 и У'i
-устойчивые состояния, исходное и после
окончания переходного процесса. Переход из
состояния У'i-1 под воздействием Xi
в У'i происходит однозначно и не зависит
от порядка переключения сигналов.
У'i. Будем
считать переход корректным, если он свободен от
генерации, критических состязаний сигналов и
риска сбоя. Обычно граф корректного перехода
описывается следующим образом: У'i-1 и У'i
-устойчивые состояния, исходное и после
окончания переходного процесса. Переход из
состояния У'i-1 под воздействием Xi
в У'i происходит однозначно и не зависит
от порядка переключения сигналов.

рис 2.
Граф корректного перехода. У — состояние
схемы, X— входное воздействие.
Предлагаемая в настоящей
работе модель корректного переключени
основывается на детализации процесса
переключения. Состояние, достигнутое схемой в
результате переключения, имеет две составляющие:
- У*i
- значения элементов памяти,
выработанные на переходе в состояние
- У'i;
Уi - значения элементов
памяти, сохранившиеся на переходе от состояния У'i-1
к У'i.
- Вновь достигнутое состояние схемы устойчиво
хранится, хотя в общем случае хранению подлежат
не все значения элементов памяти, что выражается
соотношением Уi
 У*i
У*i  У'i.
У'i.
Вектор входных переменных имеет
следующие составляющие:
- Хi --
сигналы, обеспечивающие хранение Уi
- Уi;Х*i --
сигналы, обеспечивающие
совместно с Уi и Хi установку
значений
- У*i; Х'i- сигналы, обеспечивающие
хранение У'i.
- Каждый из элементов памяти включен либо в У*,
либо в У.
В пределах переключающего набора
должны быть обеспечены хранение Уi,
установка У*i и хранение У'i, что может
быть выполнено, только если справедливо
соотношение Xi X*i
X*i Х'i
Х'i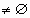 . Здесь не
исключается, что один и тот же вход схемы может
участвовать как в установке У*i, так и в
любом из хранений Уi или У'i. Предлагаемая
модель переключения с учетом введенных
обозначений представлена на рис.3; переключение в
общем случае происходит в два набора.
. Здесь не
исключается, что один и тот же вход схемы может
участвовать как в установке У*i, так и в
любом из хранений Уi или У'i. Предлагаемая
модель переключения с учетом введенных
обозначений представлена на рис.3; переключение в
общем случае происходит в два набора.
Нейтральный набор. Входное
воздействие Х'i-1 на протяжении
переходного процесса устойчиво хранит состояние
У'i-1. Входное воздействие Хi хранит
состоние Уi, причем У'i-1 Уi. Набор назван
нейтральным, так как в нем действуют два момента
хранения, а состояние схемы физически не
изменяется и остается равным У'i-1,
достигнутому в предыдущем наборе. Нейтральный
набор осуществляет подготовку к последующему
переключению за счет формального перехода к
более свободному состоянию Уi.
Уi. Набор назван
нейтральным, так как в нем действуют два момента
хранения, а состояние схемы физически не
изменяется и остается равным У'i-1,
достигнутому в предыдущем наборе. Нейтральный
набор осуществляет подготовку к последующему
переключению за счет формального перехода к
более свободному состоянию Уi.
Переключающий набор. Входное
воздействие Хi на протяжении
переходного процесса устойчиво хранит состояние
Уi. Входное воздействие Х*i при
участии хранящихся сигналов Уi
устанавливает элементы памяти у*ik = р. Схема
оказывается в состонии Уi У*i, а затем переходит в
окончательное устойчивое состояние У'i, Уi
У*i, а затем переходит в
окончательное устойчивое состояние У'i, Уi У*i
У*i  У'i , устойчивость
У'i обеспечивается входным
воздействием Х'i. Набор назван
переключающим, поскольку в нем вырабатываются
элемент памяти из У*i.
У'i , устойчивость
У'i обеспечивается входным
воздействием Х'i. Набор назван
переключающим, поскольку в нем вырабатываются
элемент памяти из У*i.
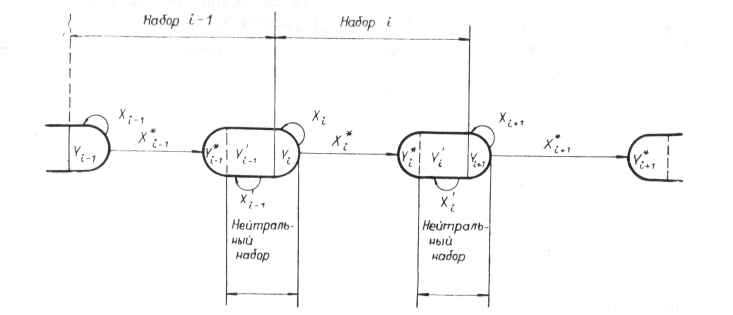
Рис.3. Модель корректного перехода -
пояснение см. в тексте
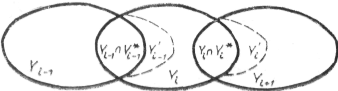
Рис.4. Диаграмма переходов по состоянию.
Диаграмма переходов по состоянию в
принятой модели переключения представлена на
рис.4.
Переключения входов и соответствующие
им изменения состояния схемы можно сопоставить с
помощью следующей схемы:
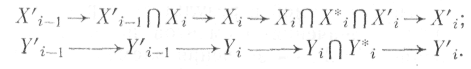
Сформулируем правила формировани
переключающего и нейтрального наборов.
Правило 1. Нейтральный набор
образуется следующим образом:
- входы равны Х'i
 Xi
Xi
- состояние равно У'i-1
Правило 2. Переключающий набор
образуется следующим образом:
- входы равны Xi
 X*i
X*i Х'i,
Х'i,
- состоние равно Уi
 У*i.
У*i.
Чтобы можно, было получить наборы в
соответствии со сформулированными правилами,
необходимо выполнение следующих условий:
Отметим, что если выполнено условие Х'i-1 Хi, то
нейтральный набор не нужен.
Хi, то
нейтральный набор не нужен.
В случае Уi У*i = У'i условия корректного
переключения имеют следующий вид:
У*i = У'i условия корректного
переключения имеют следующий вид:
- Уi=
У'i/ У'i-1;
- Xi Уi Уi
 c,c
c,c Cp(Yi);
Cp(Yi);
Х'i-1 У'i-1 У'i-1 d,d
d,d Cp(У'i-1)
Cp(У'i-1)
- X*i Уi У'i
 e,e
e,e Cx(У'i)
Cx(У'i)
- У*i ациклично.
Сформулируем критерий корректности
переключения состояния, когда
последовательность состоит из наборов,
построенных по правилам 1 и 2.
Теорема 3. Переход от состояния У'i-1
к состоянию У'i корректен тогда и только
тогда, когда выполнены условия 1)—4).
При Уi У*i
У*i У'i дл у*ik
= р достаточно переписать условие 4) в виде XiУi(Уi
У'i дл у*ik
= р достаточно переписать условие 4) в виде XiУi(Уi У*i)
У*i) e,e
e,e Cx(Уi
Cx(Уi У*i). Все
рассуждения остаются справедливыми. Для yik=p
в соответствии с условием 2) обеспечена
устойчивость на переходе, а по правилу 2 входное
воздействие содержит составляющую Хi, что
обеспечивает устойчивость yik =p в
наборе.
У*i). Все
рассуждения остаются справедливыми. Для yik=p
в соответствии с условием 2) обеспечена
устойчивость на переходе, а по правилу 2 входное
воздействие содержит составляющую Хi, что
обеспечивает устойчивость yik =p в
наборе.
Пример. Рассмотрим схему,
представленную на рис. 1. Запишем два
переключающих набора в формате
- F= (x1x2x3x4x5x6y1y2y3)
- набор 1 (0, 1, х, х, 0, х, 1, х, х)
- набор 2 (х, 0, х, х, 1, 1, 1, х, 1).
тогда составляющие набора 1 имеют
следующий вид:
- У'1 = 1хх, Х'1 = х1хххх,
c1 = 1хх,
- Х*1=0ххх0х,
У1=xxx, причем
последнее означает, что набор 1 является
установочным набором.
Составляющие набора 2 имеют следующий
вид:
- У'2=1x1,
Х'2= хххх11,
- У*2= хх1, Х*2 = х0хх1х,
- У2=1хх, Х2 = хххх1х.
Из того, что У'2/У'1 = У2,
Х'1 Х2
Х2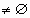 , Х'1
, Х'1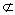 Х2, следует,
что переход от набора 1 к набору 2 через
нейтральный набор, сформированный по правилу 1,
корректен. Окончательно корректна
последовательность, записанная в формате F, имеет
следующий вид:
Х2, следует,
что переход от набора 1 к набору 2 через
нейтральный набор, сформированный по правилу 1,
корректен. Окончательно корректна
последовательность, записанная в формате F, имеет
следующий вид:
№ набора |
Составляющие |
результат |
1 |
Х*1 Х'1 У1 Х'1 У1 У*1=0 1 х х
0 х 1 х х У*1=0 1 х х
0 х 1 х х |
2 |
Х'1 Х2 У'1=
x 1 х х 1 х 1 х х Х2 У'1=
x 1 х х 1 х 1 х х |
3 |
Х2 Х*2 Х*2 Х'2 У2 Х'2 У2 У*2 =х 0 х
х 1 1 1 х 1 У*2 =х 0 х
х 1 1 1 х 1 |
Заключение
Использование доказанной в работе
теоремы 3 при синтезе наборов теста гарантирует
отсутствие риска сбоя, гонок и критических
состязаний в последовательностях. Услови
теоремы легли в основу машинноориентированного
регулярного метода синтеза теста.
Синтезированные последовательности не требуют
последующего анализа на корректность, как это
делается в случайных и эвристических методах
синтеза.
Рассмотренный метод применим к
комбинационным схемам и к таким
последовательностным схемам, для которых могут
быть построены наборы, корректные по результатам
троичного моделирования. Приведенные в
настоящей работе теоремы показывают, что аппарат
исчисления кубических комплексов может
применяться для синтеза корректных
последовательностей.
Процедура синтеза корректных
последовательностей реализована в системе
проектирования тестов на ЕС ЭВМ.
Приложение
Доказательство монотонности
функции g. ЕслиB Np,
p
Np,
p {0,1}, то из
определени комплексов N0,N1 можно
заключить, что A
{0,1}, то из
определени комплексов N0,N1 можно
заключить, что A Np
и, следовательно, g(В)=g(A)=p. Если B
Np
и, следовательно, g(В)=g(A)=p. Если B Nx, то либо A
Nx, то либо A Nx и тогда g(В)=g(A)=x,
либо A
Nx и тогда g(В)=g(A)=x,
либо A Np и тогда
g(В) =х, g(А)=р и, следовательно, g(А)
Np и тогда
g(В) =х, g(А)=р и, следовательно, g(А)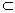 g(В). Таким образом,
если A
g(В). Таким образом,
если A B, то и g(А)
B, то и g(А) g(В), что и
требовалось доказать.
g(В), что и
требовалось доказать.
Доказательство необходимости
теоремы 1. Предположим, что выход схемы
изменяется, но g(A/В) =р и функция g монотонна.
Вследствие этого если g(А/В)=р, то g(А)=р, g(В)=p,
что противоречит сделанному предположению.
Доказательство достаточности
теоремы 1. Изменение выхода схемы означает, что
g(А)=р, g(В)=р. Из монотонности g и
определения покоординатной операции вычислени
переходного вектора следует, что g(А/В)=х.
Доказательство теоремы 2. По
условиям теоремы g(А)=р и g(В)=р. Статический
риск сбоя означает, что выход схемы изменяется на
переходе от набора А к набору В. По
теореме 1 изменение выхода имеет место тогда и
только тогда, когда g(А/В) =х, а по определению
функции g это означает, что А/В Nx , что и
требовалось доказать.
Nx , что и
требовалось доказать.
Для доказательства теоремы 3
понадобится следующая лемма.
Лемма. Если А В
В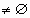 ,
Н
,
Н L
L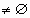 и H
и H A,
то (А
A,
то (А В)/( Н
В)/( Н L)
L)  A.
A.
Доказательство: А В
В A, Н
A, Н L
L H, откуда следует, что Н
H, откуда следует, что Н L
L А. По определению покоординатной
операции вычислени переходного вектора (А
А. По определению покоординатной
операции вычислени переходного вектора (А В)/(Н
В)/(Н L)
L) A,
что и требовалось доказать.
A,
что и требовалось доказать.
Доказательство достаточности
теоремы 3. Рассмотрим переход из состояния У'i-1
в состояние У'i. Пусть для Х'i-1 и
Хi справедливо соотношение Х'i-1 Хi. Формируем
последовательность, состоящую из двух
переключающих наборов:
Хi. Формируем
последовательность, состоящую из двух
переключающих наборов:
Вычислим переходный вектор. Так как Х'i-1 Хi, то в
соответствии с леммой (Хi-1
Хi, то в
соответствии с леммой (Хi-1 Х*i-1
Х*i-1 Х'i-1)/( Хi
Х'i-1)/( Хi Х*i
Х*i Х'i)
Х'i)
 Хi, а в
соответствии с условием 1) У'i-1/У'i
= Уi. Так как условие 2) выполнено, то
согласно следствию 2 из теоремы 2 сигналы
обратной связи хранятся на переходе без
статического риска сбоя. Согласно условию 4) и
теореме 5 работы [3] любой y*ik =p
вырабатывается без критических состязаний.
Устойчивость конечного состояния У'i следует
из выполнения условия 3). Пусть для Х'i-1 и
Хi справедливо соотношение Х'i-1
Хi, а в
соответствии с условием 1) У'i-1/У'i
= Уi. Так как условие 2) выполнено, то
согласно следствию 2 из теоремы 2 сигналы
обратной связи хранятся на переходе без
статического риска сбоя. Согласно условию 4) и
теореме 5 работы [3] любой y*ik =p
вырабатывается без критических состязаний.
Устойчивость конечного состояния У'i следует
из выполнения условия 3). Пусть для Х'i-1 и
Хi справедливо соотношение Х'i-1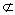 Xi , тогда
формируем последовательность, состоящую из трех
наборов:
Xi , тогда
формируем последовательность, состоящую из трех
наборов:
Вычислим переходный вектор дл первого
перехода. В соответствии с леммой (Х'i-1 Хi)/(Хi-1
Хi)/(Хi-1 Х*i-1
Х*i-1 Х'i-1)
Х'i-1) Х'i-1, а У'i-1/
У'i-1 = У'i-1 . По условию 3) и согласно
следствию 2 из теоремы 2 У'i-1 хранится на
переходе без статического риска сбоя. Для
второго перехода по лемме и условию 1) переходный
вектор включен в Хi Уi и,
следовательно, доказательство сводится к уже
рассмотренному случаю. Таким образом, доказана
достаточность условий 1)—4).
Х'i-1, а У'i-1/
У'i-1 = У'i-1 . По условию 3) и согласно
следствию 2 из теоремы 2 У'i-1 хранится на
переходе без статического риска сбоя. Для
второго перехода по лемме и условию 1) переходный
вектор включен в Хi Уi и,
следовательно, доказательство сводится к уже
рассмотренному случаю. Таким образом, доказана
достаточность условий 1)—4).
Доказательство необходимости
теоремы 3. Рассмотрим переключающий набор. Из
того, что сигналы обратной связи должны
храниться на переходе без статического риска
сбоя, следует необходимость условий (1) и (2).
Выработанное состояние должно устойчиво
храниться, что обусловливает необходимость
условия (3). Наконец, при выработке значений
сигналов обратной связи должны отсутствовать
критические состязания; из этого положени
следует необходимость условия (4). Для случая с
нейтральным набором нетрудно провести
аналогичные рассуждения.
СПИСОК ЛИТЕРАТУРЫ
- Майоров С. А., Новиков Г. И., Немолочнов О. Ф.,
Баранов С. И., Шипилов П. А.,Скорубский В. И.,
Петухов Г. А., Тимченко Б. Д.
Проектирование
цифровых вычислительных машин. «Высшая школа»,
1972. 343 с.
- Миллер Р.
Теория переключательных схем. Т. 1.
«Наука», 1970. 416 с.
- Немолочнов О. Ф., Усвятский А. Е.
Метод анализа
состязаний по кубическим покрытиям логических
схем. — Автоматика и телемеханика, 1977, № 2, с. 126—135
- Немолочнов О. Ф.
Методы технической
диагностики. Методические указания к курсовой
работе. Л., 1978. 68 с.
- Рutzоlи G. К., Rоth
J. Р. А heuristic algorithm for the
testing of asinchronous circuits.-IEEE Trans.,1971,vol.C-20,N 6, p. 639-647.
- Немолочнов О. Ф.
Анализ и устранение
критических состязаний сигналов при синтезе
тестовых последовательностей. — Автоматика и
телемеханика, 1976, № 11, с. 173-181.
Поступила в редакцию 28.11.78