Рекомендации
к выполнению
лабораторных работ
по курсу
«Контроль и
диагностика ЭВМ»
(доц., к.т.н. Виктор
Фомич Звягин ауд. 366)
[ рассматривается
пример выполнения одного из вариантов]
Введение.
Рассмотрение каждой из
лабораторных работ состоит из 3х разделов:
• Теория
– необходимый теоретический материал.
• Рекомендации
– включает в себя рекомендации студентов по выполнению практической части.
• Практика
– пример из лабораторной работы
При составлении рекомендаций
использованы следующие материалы:
• Практикум
по курсу Контроль и диагностика ЭВМ
•
В. Н. Голыничев,
В. Ф. Звягин. Анализ и контроль логических схем. Учебное пособие.
(в формате MS Word)
!!!
ВНИМАНИЕ !!!
Перед составлением схем и
практической работой с TW-CAD ВНИМАТЕЛЬНО ознакомьтесь с документацией и
правилами синтаксиса. Это поможет Вам избавиться от огромного количества
вопросов по работоспособности программы и существенно сэкономит время.
Содержание.
Лабораторная
работа № 1. Описание схемы и верификация проекта методом двоичного
моделирования
ТЕОРИЯ.
РЕКОМЕНДАЦИИ
по описанию схемы
ПРИМЕР.
РЕКОМЕНДАЦИИ по
верификации схемы методом двоичного моделирования
ПРИМЕР
Лабораторная
работа № 2. Троичное
моделирование - анализ переходов
ТЕОРИЯ.
РЕКОМЕНДАЦИИ
общие.
ПРИМЕР.
Лабораторная
работа № 3. П-алгоритм – метод
анализа схем.
ТЕОРИЯ.
РЕКОМЕНДАЦИИ
общие
ПРИМЕР.
Лабораторная
работа № 4. Проектирование теста
по кубическим покрытиям
РЕКОМЕНДАЦИИ.
ПРИМЕР.
Лабораторная
работа № 6. Тестовое обеспечение
и тестопригодное проектирование
ТЕОРИЯ.
РЕКОМЕНДАЦИИ
общие
РЕКОМЕНДАЦИИ
по описанию базовой схемы
РЕКОМЕНДАЦИИ
по описанию модифицированных схем и их анализу
РЕКОМЕНДАЦИИ
по проектированию теста
ПРИМЕР.
Описание схемы и
верификация проекта методом двоичного моделирования
Машинно-ориентированная
математическая модель логической схемы.
Логическая схема в САПР
представляется математической моделью. В качестве математической модели
логической схемы может быть использована система булевых функций. В
системе каждая функция описывает поведение отдельного выхода, зависящего
от входных переменных и переменных, определяющих состояние схемы. Такой
системой удобно представлять простые схемы. С увеличением
сложности схем число термов в системе становится слишком большим. Для того,
чтобы понизить размерность задачи, выполняют декомпозицию логической схемы. В
результате декомпозиции схема разбивается на одновыходные
подсхемы, а в системе появляются промежуточные переменные,
соответствующие выходам подсхем. В такой системе имеет место сумма числа
термов, а не их произведение. В логической схеме всегда можно выделить
элементы памяти - последовательностную часть схемы и
комбинационную, например так, как это показано на рис.
1.1. В последовательностной части схемы в качестве подсхемы
выберем отдельные триггеры. В комбинационной части схемы подсхемы
выбирают с учетом ограничений на количество переменных и термов.
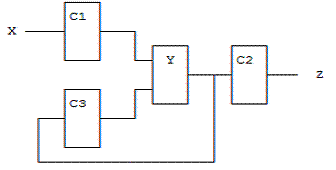
Рис. 1.1. Логическая
схема с выделенной последовательностной и комбинационной
частью: X - независимые входы схемы, C1 - входная логика, Y -
элементы памяти, C2 - выходная логика, C3 - функции возбуждения, Z - выходы
схемы
Двоичное моделирование
Двоичное моделирование
является самым простым и быстродействующим. Все входные сигналы схемы
записывают в алфавите {0,1}. Моделирование комбинационной схемы состоит в
вычислении, в порядке возрастания рангов, значений на выходе элементов схемы.
Если у вентиля определены сигналы на всех его входах, то двоичное значение на
выходе этого вентиля может быть определено по его кубическому покрытию. Как уже
отмечалось, упорядочение вычислений (схема предварительно
ранжируется) обеспечивает вычисление состояний элементов
комбинационной схемы за один просчет (итерацию) для каждого набора входной
последовательности.
В качестве примера
рассмотрим двоичное моделирование комбинационной схемы, заданной
на уровне соединения вентилей И-НЕ (рис.
1.2,а) для последовательности, состоящей из двух наборов. Кубические
покрытия вентиля приведены на рис. 1.3,е.
Первоначально выполним ранжирование схемы. Ранг вентилей 1 и 2 схемы равен
единице. После этого может быть определен ранг вентиля 3. Он равен двум.
Начинаем моделирование набора 1 с определения состояний элементов ранга один (в
пределах одного ранга порядок вычислений безразличен). Входное
воздействие 01 на входах вентиля 1 схемы является гранью куба
нулевого покрытия вентиля, следовательно на выходе вентиля на наборе
1 будет 0. Входное воздействие 11 на входах вентиля 2 схемы равно
кубу единичного покрытия вентиля, на выходе вентиля на наборе 1 будет 1. Теперь
можно вычислять значение на выходе вентиля 3. Моделирование наборов 1 и 2
показано на рис. 1.2,б.
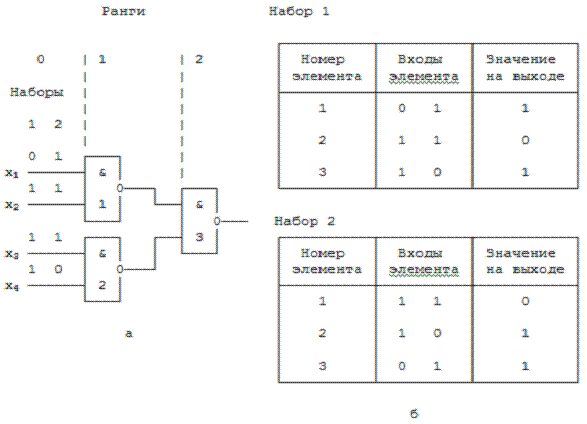
Рис 1.2.
Двоичное моделирование комбинационной схемы
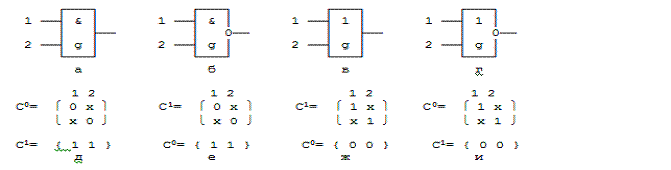
Рис. 1.3.
Двухвходовые вентили И (а), И-НЕ (б), ИЛИ (в), ИЛИ-НЕ (г) и их кубические
покрытия (д), (е), (ж), (и)
РЕКОМЕНДАЦИИ.
По предложенному кубическому
покрытию, в соответствии с вариантом, вам необходимо спроектировать логическую
схему на двухвходовых вентилях заданного базиса.
Исходное единичное покрытие С1
:
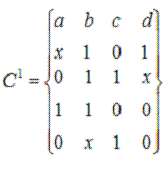
Заданный базис:
Логические элементы: И-НЕ, НЕ (инвертор)
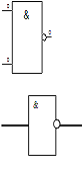
По исходному
единичному покрытию получим формулу, которую используя правила Де Моргана и
вынесение общих множителей за скобки, можно преобразовать к виду, удобному для
построения схемы на элементах заданного базиса.
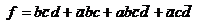
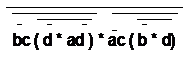
Карта
Карно:
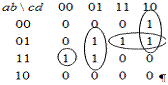
Затем, предварительно построив
схему на бумаге, пронумеруйте все вентили. Пронумеровав их, необходимо
составить описание своей схемы. Для этого, воспользовавшись шаблоном (файл cxema.ank), вы описываете
спроектированную схему в соответствии с правилами синтаксиса (см. файл cxema.ank). Результат
сохраните в файле имя_схемы.ank (пример)
Воспользовавшись
программой-ретранслятором cxema.exe, проверьте вашу схему.
В командной
строке наберите:
cxema.exe имя_схемы
В результате
будут сгенерированы следующие файлы:
·
имя_схемы.cmp – формат процедур
моделирования T,F (пример)
·
имя_схемы.rd1 – формат САПР Tw-CAD (пример)
·
имя_схемы.prn – ошибки, обнаруженные в описании схемы.
Если были обнаружены
какие-либо ошибки, проверьте еще раз описание схемы и перезапустите ретранслятор.
Схема:
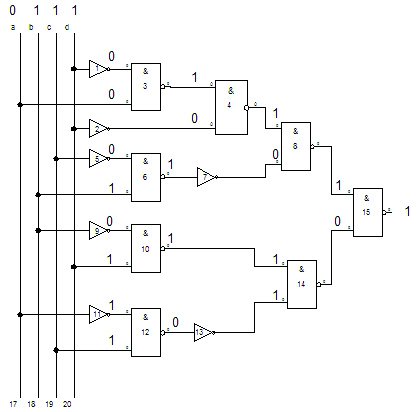
Исходный файл для ретрансляции – lab2_1.ank:
* 1 Анкета
<lab2_1>.ank - имя в уголках мелкими буквами..
11 Нумеруем c "1": сначала вентили..
затем, после кратного 16 - ..входы
*12 Число входов
в схеме <4> это 17,18,19,20
*13 Число
выходов в схеме <1> ,
*14 вот они: <15>
*15 Число
вентилей в схеме <16> - округлив 3 до кратного 16 !
*16 У вентиля < 1> типа <NI>
входных цепей < 1>
*17 <20>
*16 У вентиля < 2> типа <NI>
входных цепей < 1>
*17 <20>
*16 У вентиля < 3> типа <NI>
входных цепей < 2>
*17 <1><17>
*16 У вентиля < 4> типа <NI>
входных цепей < 2>
*17 <2><3>
*16 У вентиля < 5> типа <NI>
входных цепей < 1>
*17 <19>
*16 У вентиля < 6> типа <NI>
входных цепей < 2>
*17 <5><18>
*16 У вентиля < 7> типа <NI>
входных цепей < 1>
*17 <6>
*16 У вентиля < 8> типа <NI>
входных цепей < 2>
*17 <4><7>
*16 У вентиля < 9> типа <NI>
входных цепей < 1>
*17 <18>
*16 У вентиля < 10> типа
<NI> входных цепей < 2>
*17 <9><20>
*16 У вентиля < 11> типа
<NI> входных цепей < 1>
*17 <17>
*16 У вентиля < 12> типа
<NI> входных цепей < 2>
*17 <11><19>
*16 У вентиля < 13> типа
<NI> входных цепей < 1>
*17 <12>
*16 У вентиля < 14> типа
<NI> входных цепей < 2>
*17 <10><13>
*16 У вентиля < 15> типа
<NI> входных цепей < 2>
*17 <8><14>
Файл
для программы моделирования от СХЕМА (формат PCAD)
– lab2_1.cmp:
lab2_1 (
)
BEGIN
NI :
1 ( X 1
=20, Y 0 =1
)
NI :
2 ( X 1
=20, Y 0 =2
)
NI :
3 ( X 1
=1, X 2
=17,
( Y 0 =3 )
NI :
4 ( X 1
=2, X 2
=3,
( Y 0 =4 )
NI :
5 ( X 1
=19, Y 0 =5
)
NI :
6 ( X 1
=5, X 2
=18,
( Y 0 =6 )
NI :
7 ( X 1
=6, Y 0 =7 )
NI :
8 ( X 1
=4, X 2
=7,
( Y 0 =8 )
NI :
9 ( X 1
=18, Y 0 =9
)
NI
:10 ( X
1 =9, X
2 =20,
( Y 0 =10 )
NI
:11 ( X
1 =17, Y
0 =11 )
NI
:12 ( X
1 =11, X
2 =19,
( Y 0 =12 )
NI
:13 ( X
1 =12, Y
0 =13 )
NI
:14 ( X
1 =10, X 2
=13,
( Y 0 =14 )
NI
:15 ( X
1 =8, X
2 =14,
( Y 0 =15 )
PORT1:
1 ( X 1
=17, X 2
=18,
( X 3 =19, X 4
=20 )
PORT2:
2 ( X 5
=15 )
END
Файл
для САПР Tw-CAD – lab2_1.rd1:
* схема для Tw-CAD
ПЛАТА:
lab2_1 ;
НЕИ -
1: 1/20, 25/ 1 ;
НЕИ -
2: 1/20, 25/ 2 ;
НЕИ -
3: 1/ 1, 2/17, 25/ 3 ;
НЕИ -
4: 1/ 2, 2/ 3, 25/ 4 ;
НЕИ -
5: 1/19, 25/ 5 ;
НЕИ -
6: 1/ 5, 2/18, 25/ 6 ;
НЕИ -
7: 1/ 6, 25/ 7 ;
НЕИ -
8: 1/ 4, 2/ 7, 25/ 8 ;
НЕИ -
9: 1/18, 25/ 9 ;
НЕИ
-10: 1/ 9, 2/20, 25/10 ;
НЕИ
-11: 1/17, 25/11 ;
НЕИ
-12: 1/11, 2/19, 25/12 ;
НЕИ
-13: 1/12, 25/13 ;
НЕИ
-14: 1/10, 2/13, 25/14 ;
НЕИ
-15: 1/ 8, 2/14, 25/15 ;
KOЛOДKA-IN: 1/17, 2/18, 3/19, 4/20 ;
КОЛОДКА-EX: 5/15 ;
На следующем этапе вам нужно
выполнить верификацию проекта методом двоичного моделирования, иначе говоря,
показать, что схема действительно реализует заданную булеву функцию:
- на тривиальном тесте из 16
наборов для проверки таблицы истинности;
- на 4 кубах заданного
кубического покрытия;
- на кубах покрытия, инверсного
заданному, составленному по карте Карно.
Для этого:
- Запустите пакетный файл f.bat, набрав в
командной строке:
f.bat имя_схемы
имя_файла_результата
Примечание. имя_схемы – имя файла с расширением cmp, который был создан на предыдущем этапе, НО без указания расширения.
Далее вам
будет предложено ввести количество тестовых наборов и сами тестовые наборы:
- Тривиальный тестовый набор
(состоит из 16ти значений: 0000 … 1111)
- Тестовый набор из кубов
заданного покрытия (в зависимости от варианта)
- Кубы покрытия, инверсного
заданному (в зависимости от варианта).
Покрытие С0, инверсное
заданному, полученное по карте Карно: 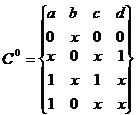
Карта Карно:
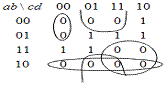
Проверка на тесте из 16
наборов:
***
ДВОИЧНОЕ МОДЕЛИРОВАНИЕ ***
No
набоpа Входные контакты Выходные контакты
1
0000
0
2
0001
0
3
0010
1
4
0011
0
5
0100
0
6
0101
1
7
0110
1
8
0111
1
9 1000
0
10
1001
0
11
1010
0
12
1011
0
13
1100
1
14
1101
1
15
1110
0
16
1111
0
******* Работа
завеpшена *******
Проверка
на тесте из 4 кубов заданного кубического покрытия:
***
ДВОИЧНОЕ МОДЕЛИРОВАНИЕ ***
No
набоpа Входные контакты Выходные контакты
1
x101
1
2
011x
1
3
1100
1
4
0x10
1
******* Работа
завеpшена *******
Проверка на тесте из кубов
“0”-го покрытия:
*** ДВОИЧНОЕ МОДЕЛИРОВАНИЕ
***
No набоpа Входные
контакты Выходные контакты
1
0x00
0
2
x0x1
0
3
1x1x
0
4
10xx
0
******* Работа завеpшена *******
Троичное
моделирование - анализ переходов
Задержки и риски сбоя
Сигналы в любом цифровом
устройстве распространяются с некоторой задержкой, обусловленной
быстродействием элементов и задержкой распространения сигналов в соединительных
проводниках. Типовое, минимальное и максимальное значения времени задержки
распространения сигнала через компоненту приводятся в паспортных
данных. Входы одной и той же компоненты могут иметь разные задержки. Могут
различаться величины задержек при разных переключениях 0→ 1 и 1→ 0.
В высокоскоростных устройствах необходимо принимать в расчет величины задержек
соединительных проводников, пропорциональных погонной емкости.
Различают два типа
задержек. Совершенную величиной δ, которая задерживает
входной сигнал f(t) на время δ без изменения формы входного сигнала.
Инерционную величиной δ, которая изменяет выходной
сигнал, только если входной сигнал не изменяется в течение времени
δ. На рис. 2.1 показаны временные
диаграммы для случаев совершенной и инерционной задержек.
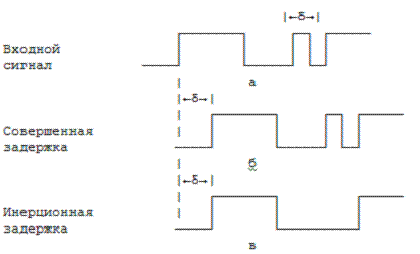
Рис. 2.1.
Временные диаграммы совершенной и инерционной задержек величины d. Форма
входного сигнала (а), форма выходного сигнала совершенной задержки (б),
форма выходного сигнала инерционной задержки (в)
Рассмотрим влияние
задержек на переходный процесс в комбинационной схеме при смене входных
воздействий. Говорят, что в комбинационной схеме существует
риск сбоя, если можно найти такую комбинацию задержек
распространения изменения входных сигналов, при которой на выходе схемы
может появиться ложный импульс.
Риск сбоя в
комбинационной схеме бывает статическим или динамическим.
Риск сбоя называют статическим, если выходное значение должно
сохраняться постоянным при смене входных воздействий, но при некоторой
комбинации задержек в переходном процессе на выходе может появиться один
или более импульсов. То есть выходное значение изменится четное
число раз (рис. 2.2).
Различают статический риск сбоя в нуле, если выход должен сохраниться в нуле (рис. 2.2,а) и риск сбоя в единице, если выход должен
сохраниться в единице (рис. 2.2,б).
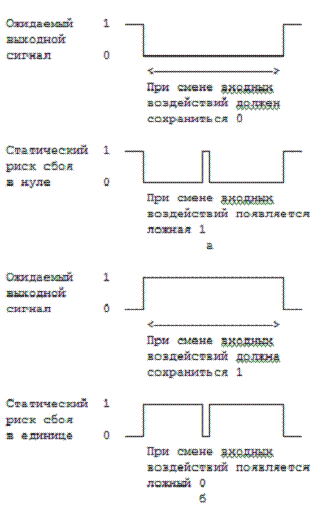
Рис. 2.2.
Статический риск сбоя: а - в нуле; б - в единице
Появление статического
риска сбоя при смене входных воздействий проиллюстрируем на примере
двухвходовых вентилей. Рассмотрим работу вентилей типа И и типа ИЛИ
исходя из того, что сигналы на входах не могут измениться
одновременно. Пусть сигнал на входе 1 вентиля изменяется из 0 в 1, а
сигнал на входе 2 из 1 в 0. Как воздействие 01, так и воздействие
10 вырабатывают 0 на выходе вентиля И и 1 на выходе вентиля ИЛИ.
Возможны два варианта. Если сигнал на входе 1 изменится раньше чем
сигнал на входе 2, то на выходе вентиля И появится ложная единица. Если
сигнал на входе 1 изменится позже, чем сигнал на входе 2, то
на выходе вентиля И ложная единица не появится (рис. 2.3,а). Двойственная ситуация для риска
сбоя в единице показана на примере вентиля ИЛИ (рис. 2.3,б).
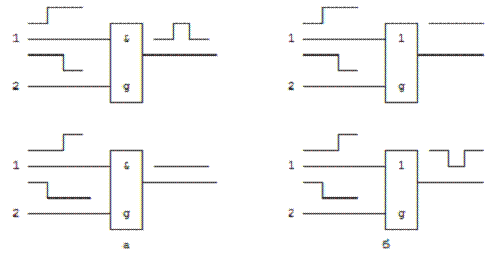
Рис. 2.3.
Статический риск сбоя на выходе двухвходовых вентилей при изменении входных
сигналов: а - в нуле; б - в единице
Динамический риск сбоя соответствует
трехкратной (или большей нечетной) смене выходного сигнала, тогда
как требуется лишь одно такое изменение (рис.2.4.).
Динамический риск сбоя является следствием статического риска сбоя.
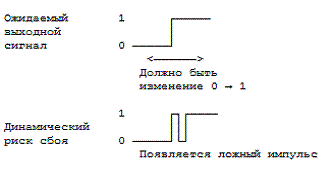
Рис. 2.4. Динамический риск сбоя
Риск сбоя - это только
возможность ложного срабатывания схемы. В конкретном экземпляре цифрового
устройства комбинация значений задержек может не приводить к ложным
срабатываниям. Появление ложного импульса на выходе комбинационной
схемы может быть опасным. Опасна возможность запоминания ложного импульса в
триггере.
Троичное моделирование
Эйхельбергером предложен
способ анализа состязаний с помощью моделирования, базирующегося на
использовании алфавита {0, 1, x}. Основное назначение троичного моделирования -
выявить состязания сигналов, вызванные неодновременностью смены входов и
неодновременностью переключений элементов схемы. Символ x в троичном моделировании
обозначает изменяющийся сигнал. Это может быть изменение сигнала при
смене входных воздействий, появление на короткое время
ложного сигнала (статический или динамический риск сбоя),
генерация сигнала. Расширение значности алфавита с двух
символов до трех обуславливает меньшее быстродействие процедуры троичного
моделирования по сравнению с двоичным моделированием. Однако, когда в
результате троичного моделирования вычислены значения сигналов, равные 0 или 1,
то это означает, что если правильное функционирование логической схемы не
основывается на специальном подборе задержек, результаты троичного
моделирования адекватны работе схемы. Троичное моделирование заслуживает
внимания, поскольку оно, в отличие от двоичного моделирования, позволяет
выявить состязания сигналов при произвольном распределении задержек в схеме.
Опираясь на вышеизложенную
теорию, попытайтесь обнаружить по вашей карте Карно:
- 2 перехода, свободных от риска сбоя;
- 2 перехода с функциональным риском сбоя, который можно
обойти;
- 2 цепочки наборов в обход выбранных переходов с
функциональным риском сбоя;
- 2 цепочки без риска сбоя в обход риска сбоя, указанного в
пункте 2;
- 2 перехода с функциональным риском сбоя, который нельзя
обойти (если таковые имеются);
- 2 перехода с логическим риском сбоя;
- 1 переход в измененной схеме, где избавились от
логического риска сбоя.
Примечание:
если логического риска сбоя в исходной схеме нет, то, наоборот, измените
схему так, чтобы он появился.
Указания:
Выбирайте для моделирования только полностью определенные наборы,
соответствующие клеткам карты Карно, обозначая их для удобства буквами А B C
D.. Логические риски ищите только в заданном покрытии (в инверсном его просто
нет).
В отчете приведите
карту Карно с указанием переходов, на которых выполнялось моделирование, а
также сами результаты моделирования с разъяснениями. Вручную троично
промоделируйте переход с логическим риском сбоя; промоделировать дважды - для
исходной и измененной схемы. Поясните механизм появления риска сбоя и его
исчезновение при изменении схемы.
На этом этапе используется
программа model.exe.
Формат запуска программы аналогичен приведенному в
л/р№1.
После определения требуемых рисков
сбоя, необходимо смоделировать схему, где удалось избавиться от логического
риска сбоя. В отчет необходимо включить, как саму схему с покрытиями, так и все
сгенерированные фалы. Одним словом, для получившейся схемы повторить л/р №1.
Затем прогнать по схеме тест, подтверждающий, что от логического риска сбоя
удалось избавиться.
Переход, свободный от риска
сбоя.
По единичному покрытию:
0010
-> 0110
карта Карно:
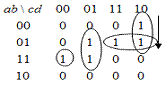
No набоpа Входные контакты
Выходные контакты
1
0010
1
*
0x10
1
2
0110
1
Переход с функциональным
риском сбоя, который можно обойти.
0010
-> 0111
карта Карно:
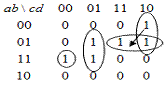
No набоpа Входные
контакты Выходные контакты
1
0010
1
* 0x1x
x
2
0111
1
Цепочка с риском сбоя в обход
риска сбоя, указанного в пункте (выше).
0010
-> 0110 -> 0111
карта Карно:
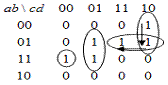
No набоpа Входные контакты
Выходные контакты
1
0010
1
*
0x10
1
2
0110
1
*
011x
1
3
0111
1
Перехода с функциональным
риском сбоя, который нельзя обойти.
0010
-> 0101
карта Карно:
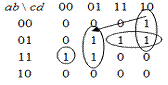
No набоpа Входные контакты
Выходные контакты
1
0010
1
*
0xxx
x
2
0101
1
Переход с логическим риском
сбоя.
0111
-> 0101
карта Карно:
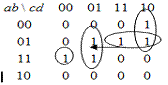
No набоpа Входные
контакты Выходные контакты
1
0111
1
* 01x1
x
2
0101
1
П-алгоритм – метод
анализа схем.
Логическую функцию одновыходной комбинационной схемы будем
представлять единичным и нулевым кубическими покрытиями,
вычисленными по p-алгоритму. Процесс
вычисления кубических покрытий по p-алгоритму
можно интерпретировать как преобразование комбинационной схемы общего
вида, заданной в виде соединения вентилей И, ИЛИ, И-НЕ, ИЛИ-НЕ, в
логически тождественную двухуровневую схему с разветвлениями только на
входах. Единичное покрытие - C1 определяет И-ИЛИ схему.
Каждому кубу c Î C1
соответствует элемент И двухуровневой схемы. Координаты куба c, отличные
от x, определяют входы элемента И. Значению координаты куба cÎ C1, равной
1, соответствует прямой вход элемента И, равной 0 - инверсный.
Нулевое покрытие - C0 определяет ИЛИ-И схему. Каждому кубу cÎ C0
соответствует элемент ИЛИ двухуровневой схемы. Координаты куба c, отличные от
x, определяют входы элемента ИЛИ. Значению координаты куба cÎ C0, равной
0, соответствует прямой вход элемента ИЛИ, равной 1 - инверсный. p -алгоритм представляет из себя процедуру
подстановки, в которой используются покрытия вентилей.
Основные типы двухвходовых вентилей и кубические покрытия,
описывающие логику их работы, приведены на рис. 1.3.
Кубические покрытия двухвходовых вентилей легко обобщить для
n-входовых вентилей.
Например, куб единичного
покрытия n-входового вентиля И будет содержать n значений 1.
Нулевое покрытие n-входового вентиля И будет содержать n кубов, в каждом
из которых очередной координате присвоено значение 0, а остальные
координаты равны x.
Исходными данными для p-алгоритма являются одновыходная
логическая схема, заданная в виде соединения вентилей, а также кубические
покрытия вентилей. Результат работы p-алгоритма
- кубическое покрытие C1 или C0, координатам кубов
которого сопоставлены входы логической схемы. Вычисление кубического покрытия
одновыходной комбинационной схемы производится по шагам.
1. Фиксируем выход
схемы в значении 1 для построения C1 или в значении 0 для
построения C0.
2. Применяем
оператор подстановки ppg, который
сопоставляет значению p , pÎ
{ 0, 1 } на выходе вентиля схемы g его кубическое покрытие Cp(g). В
кубе, содержащем p по координате, соответствующей вентилю g, p заменяется
на x, после чего куб заменяется его пересечением с Cp(g).
3. Если подстановки
выполнены не для всех вентилей схемы, шаг 2 повторяется.
В случае вычисления
кубических покрытий вручную p-алгоритм
сводится к последовательному заполнению таблицы. Столбцы таблицы
соответствуют независимым входам и выходам вентилей схемы. Число строк
определяется по мере выполнения алгоритма. Применение p-алгоритма поясним на примере вычисления
единичного и нулевого кубических покрытий для схемы, представленной на рис.
3.1. Вычисления сведены в табл 1, которая разделена
на пять граф. В графе 1 таблицы указан порядковый номер строки, сопровождаемый
символом √, если получен окончательный результат или символом ø,
если результат пересечения пуст. В графе 2 таблицы записаны
значения на входах схемы, в графе 3 значения на выходах вентилей. При
записи значений используется алфавит {0, 1, x}. В графе 4 таблицы слева
от стрелки указывается номер строки, в которую выполняется
подстановка (ссылка назад по таблице), справа от стрелки - элемент
логической схемы, для которого применяется оператор подстановки p.
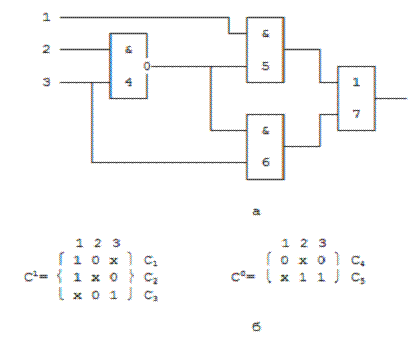
Рис. 3.1. Одновыходная
комбинационная схема (а) и кубические покрытия, описывающие логику ее работы
(б)
Например, запись вида 1¬p17v(5,6) означает,
что в строку 1 для логического значение 1 на выходе вентиля номер 7 типа
ИЛИ выполняется подстановка p17. В графе 5 таблицы указываются номера
строк, в которых записан результат пересечения данной строки
с кубическим покрытием вентиля (ссылка вперед по таблице). Графы 1,
4 и 5 таблицы носят вспомогательный характер. Записи в этих
графах позволяют контролировать ход проводимых вычислений.
Содержимое граф 2 и 3
каждой строки табл. 1 будем рассматривать как семикоординатный куб, в
котором пробел равнозначен x. На каждом шаге p-алгоритма в кубе, содержащем p
по координате, соответствующей вентилю g, p заменяется на x, после чего
куб пересекается с кубическим покрытием Cp вентиля g и
результат пересечения записывается в новые строки таблицы. В строке 1
табл. 1. записан исходный куб xxxxxx1, означающий, что ниже будет производится
вычисление единичного кубического покрытия. Применение оператора p17 состоит в замене в этом
кубе 1 на x и пересечении куба xxxxxxx с кубическим покрытием C1
вентиля 7, также записанном в семикоординатном формате.
Таблица 1
Построение
кубических покрытий C1 и C0
|
N
|
Входы
|
Вентили
|
Подстановка
|
Пере-
сечение
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|
1
|
2
|
3
|
4
|
5
|
|
1
|
|
|
|
|
|
|
1
|
Вычисление С1
|
® 2,3
|
|
2
|
|
|
|
|
1
|
x
|
|
1¬ Õ17(5,6)
|
® 4
|
|
3
|
|
|
|
|
x
|
1
|
|
® 5
|
|
4
|
1
|
|
|
1
|
|
|
|
2¬ Õ15(3,4)
|
® 6,7
|
|
5
|
|
|
1
|
1
|
|
|
|
3¬ Õ16(4,3)
|
® 8,9
|
|
6Ö
|
1
|
0
|
x
|
|
|
|
|
4¬ Õ14(2,3)
|
Рез-т
|
|
7Ö
|
1
|
x
|
0
|
|
|
|
|
Рез-т
|
|
8Ö
|
|
0
|
1
|
|
|
|
|
5¬ Õ14(2,3)
|
Рез-т
|
|
9Æ
|
|
x
|
0
|
|
|
|
|
Пусто
|
|
10
|
|
|
|
|
|
|
0
|
Вычисление С0
|
® 11
|
|
11
|
|
|
|
|
0
|
0
|
|
10¬ Õ07(5,6)
|
® 12,13
|
|
12
|
|
|
x
|
0
|
0
|
|
|
11¬ Õ06(4,3)
|
® 14,15
|
|
13
|
|
|
0
|
x
|
0
|
|
|
® 16,17
|
|
14
|
0
|
|
|
0
|
|
|
|
12¬ Õ05(3,4)
|
® 18
|
|
15
|
|
|
|
0
|
|
|
|
® 19
|
|
16Ö
|
0
|
|
0
|
x
|
|
|
|
13¬Õ05(3,4)
|
Рез-т
|
|
17
|
x
|
|
0
|
0
|
|
|
|
® 20
|
|
18Ö
|
0
|
1
|
1
|
|
|
|
|
14¬ ¬
Õ04(2,3)
|
Рез-т
|
|
19Ö
|
|
1
|
1
|
|
|
|
|
15¬ Õ04(2,3)
|
Рез-т
|
|
20Æ
|
|
1
|
0
|
|
|
|
|
17¬ Õ04(2,3)
|
Пусто
|
Единичное кубическое
покрытие вентиля 7 состоит из двух кубов, поэтому в результате
пересечения в табл. 1 будут образованы две новые строки. В графе 5
строки 1 табл. 1.8 отмечено, что результат пересечения исходного куба и
покрытия вентиля 7 схемы записан в строках 2 и 3 таблицы. Примем, что при
выполнении шага 2 p-алгоритма
координаты для подстановки будем выбирать в строке справа налево, а
очередную строку сверху вниз. Далее операторы подстановки применяются до
тех пор, пока все координаты, соответствующие выходам вентилей, не
будут равны x. В схемах общего вида, в отличие от бесповторных схем, не
все пересечения дают не пустой результат. Объясняется это наличием в
схемах сходящихся разветвлений с разной четностью инверсий в ветвях. Например,
в комбинационной схеме (рис. 1.11,а) вход 3 схемы по одной
ветви сходящегося разветвления приходит на вентиль 6 без инверсии,
а по другой через вентиль 4 с одной инверсией. В результате
подстановки p14 в строку 5 табл. 1.8
получен только один куб, а не два, так как пересечение одного из кубов
покрытия вентиля 4 с кубом из строки 5 дает пусто по входу 3
(1 ∩ 0 = Ø). Строки с пустым пересечением в дальнейших
подстановках не участвуют. Во второй части табл. 1, начиная со
строки 10, показано вычисление нулевого покрытия.
В строках табл 1,
отмеченных знаком √, графа 3 - пустая, подстановки делать не
надо. Эти кубы можно выписать в результат (см. рис. 3.2,б). В C1
выписаны все три куба, помеченные знаком √. В C0 выписаны
не три, а два куба (из строк 16 и 19). Куб, полученный в строке 18 табл.
1, является гранью куба из строки 19 и, поэтому, в нулевое покрытие не включен.
Вам требуется
освоиться с формальным методом анализа схем, позволяющим по схеме восстановить
реализованное в ней кубическое покрытие.
Построить
вручную эквивалентное дерево, а затем эквивалентное кубическое покрытие (ЭКП) в
том значении, что указано в исходном задании. ЭКП должно совпасть с результатом
автоматического построения по Tw-CAD, а после пересечения эквивалентных
координат – и с покрытием в исходном задании.
В отчете
·
эквивалентное дерево и таблица построения покрытия по П-алгоритму.
Используемые
программы из Tw-CAD:
·
работа Pialg - П-алгоритм, только кубы без противоречий,
·
работа P - П-алгоритм, все кубы, включая противоречивые.
В
качестве совета: Если кубов в покрытии десятки, то это повод задуматься
насколько хорошо Вы реализовали схему. Вполне возможно, что придется
переделывать предыдущие работы, т.к. наличие большого количества кубов вызовет
значительные затруднения при выполнении следующей работы.
Файлы,
используемые в работе, после запуска программ:
·
Эквивалентное дерево – файл tspr.t11
·
Покрытия с противоречиями (программа p) –
файл tspr.t10
·
Покрытие без противоречивых кубов (программа pialg)–
файл tspr.t21
Получив
требуемые покрытия, приведите их к более читаемому виду, чтобы удостовериться в
том, что единичное покрытие, полученное каждой из программ (p и pialg),
полностью совпало с исходным.
Таблица построения покрытия по
П-алгоритму.
|
N
|
Входы
|
Вентили
|
Подстановка
|
Пере-
сечение
|
|
17
|
18
|
19
|
20
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
15
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
Вычисление
С1
|
® 2,3
|
|
2
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|
|
|
|
|
x
|
|
1¬ Õ115(8,14)
|
® 4
|
|
3
|
|
|
|
|
|
|
|
|
|
|
|
x
|
|
|
|
|
|
0
|
|
® 5
|
|
4
|
|
|
|
|
|
|
|
1
|
|
|
1
|
|
|
|
|
|
|
|
|
2¬ Õ18(4,7)
|
® 6,7
|
|
5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
1
|
|
|
3¬ Õ114(10,13)
|
® 8,9
|
|
6
|
|
|
|
|
|
0
|
x
|
|
|
|
1
|
|
|
|
|
|
|
|
|
4¬ Õ14(2,3)
|
® 10
|
|
7
|
|
|
|
|
|
x
|
0
|
|
|
|
1
|
|
|
|
|
|
|
|
|
® 11
|
|
8
|
|
|
|
0
|
|
|
|
|
|
|
|
|
x
|
|
|
|
1
|
|
|
5¬ Õ110(20,9)
|
® 12
|
|
9
|
|
|
|
x
|
|
|
|
|
|
|
|
|
0
|
|
|
|
1
|
|
|
® 13
|
|
10
|
|
|
|
1
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
6¬ Õ12(20)
|
® 14
|
|
11
|
1
|
|
|
|
1
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
7¬ Õ13(17,1)
|
® 15
|
|
12
|
|
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|
|
|
8¬ Õ113(12)
|
® 16
|
|
13
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
9¬ Õ19(18)
|
® 17
|
|
14
|
|
|
|
1
|
|
|
|
|
|
0
|
|
|
|
|
|
|
|
|
|
10¬ Õ17(6)
|
® 18
|
|
15
|
1
|
|
|
0
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
11¬ Õ11(20)
|
® 19
|
|
16
|
|
|
1
|
0
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
12¬ Õ112(19,11)
|
® 20
|
|
17
|
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
|
|
|
13¬ Õ113(12)
|
® 21
|
|
18
|
|
1
|
|
1
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
14¬ Õ16(18,5)
|
® 22
|
|
19
|
1
|
|
|
0
|
|
|
|
|
|
0
|
|
|
|
|
|
|
|
|
|
15¬ Õ17(6)
|
® 23
|
|
20Ö
|
0
|
x
|
1
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16¬ Õ111(17)
|
Рез-т
|
|
21
|
|
1
|
1
|
|
|
|
|
|
|
|
|
|
|
|
1
|
|
|
|
|
17¬ Õ112(19,11)
|
® 24
|
|
22Ö
|
x
|
1
|
0
|
1
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18¬ Õ15(19)
|
Рез-т
|
|
23
|
1
|
1
|
|
0
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
|
|
19¬ Õ16(18,5)
|
® 25
|
|
24Ö
|
0
|
1
|
1
|
x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20¬ Õ111(17)
|
Рез-т
|
|
25Ö
|
1
|
1
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21¬ Õ15(19)
|
Рез-т
|
Результаты pialg:
шаг номер
25 1: кубические покрытия без
противоречивых кубов
Э K B И B A Л E H T H Ы E K У Б И Ч E C K И
E П O K P Ы T И Я C X E M Ы LAB2_1
1 2 3 4
5 6 7 8
9
ФOPMAT
MAKPO 1: 20 20
17 19 18 18 20
17 19
HEИ-15:25 =>EX 5
1(
15.1, 0.0 )
ЭKBИBAЛETHOE KУБИЧECKOE ПOKPЫTИE
(AДPEC= 1 KУБOB
6 значение 0)
123456789
123456789
123456789 123456789
1
0x0xxxxx0
xxx1x01xx
xxx1xxx1x xxxx001xx
5
xxxx0xx1x xxxx0xxx0
ЭKBИBAЛETHOE KУБИЧECKOE ПOKPЫTИE
(AДPEC= 7 KУБOB
4 значение 1)
123456789
123456789
123456789 123456789
7
1xx01xxxx
x0101xxxx
xxxxx1x01 xxxxxx001
Преобразуем к более читаемому
виду кубы единичного покрытия:
|
|
20
d
|
20
d
|
17
a
|
19
c
|
18
b
|
18
b
|
20
d
|
17
a
|
19
c
|
|
C7
|
1
|
x
|
x
|
0
|
1
|
x
|
x
|
x
|
x
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
|
C9
|
x
|
x
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
|
C10
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
1
|
Единичное покрытие, полученное pialg:  и
и
исходное
покрытие:  полностью
совпадают
полностью
совпадают
Результаты p:
----------------------------------------------------------------------------
шаг номер 11 18: ПОКРЫТИЯ
со всеми кубами
(т.ч.противоречивыми)
Э K B И B A Л E H T H Ы E K У Б И Ч E C K И
E П O K P Ы T И Я C X E M Ы LAB2_1
1 2 3 4
5 6 7 8
9
ФOPMAT
MAKPO 1: 20 20
17 19 18 18 20
17 19
HEИ-15:25 =>EX 5
1(
15.1, 0.0 )
ЭKBИBAЛETHOE KУБИЧECKOE ПOKPЫTИE
(AДPEC= 1 KУБOB 12
значение 0)
123456789
123456789
123456789 123456789
1 01xxx01xx
01xxxxx1x
01xxxxxx0 0x0xx01xx
5
0x0xxxx1x
0x0xxxxx0
xxx1x01xx xxx1xxx1x
9
xxx1xxxx0
xxxx001xx
xxxx0xx1x xxxx0xxx0
ЭKBИBAЛETHOE KУБИЧECKOE ПOKPЫTИE
(AДPEC= 13 KУБOB 4
значение 1)
123456789 123456789
123456789
123456789
13
1xx01xxxx
x0101xxxx
xxxxx1x01 xxxxxx001
Преобразуем к более читаемому
виду кубы единичного покрытия:
|
|
20
d
|
20
d
|
17
a
|
19
c
|
18
b
|
18
b
|
20
d
|
17
a
|
19
c
|
|
C7
|
1
|
x
|
x
|
0
|
1
|
x
|
x
|
x
|
x
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
|
C9
|
x
|
x
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
|
C10
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
1
|
Единичное покрытие, полученное p:  и
и
исходное покрытие:  полностью совпадают
полностью совпадают
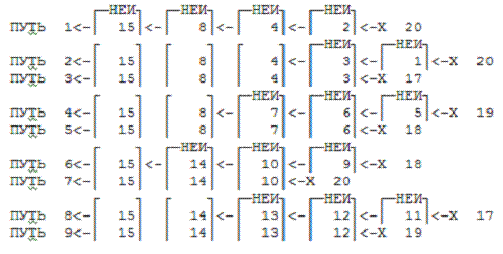
Эквивалентное дерево:
Лабораторная работа № 4.
Проектирование
теста по кубическим покрытиям
Выполняя эту
работу Вы обучитесь:
·
как формальным способом создать тест;
·
как оценить его качество;
·
как проверить свои выкладки по построению теста.
Предварительно
надо, используя программу анализа полноты теста под названием F.bat, проанализировать полноту тривиального исчерпывающего
теста из 16 наборов, чтоб узнать непроверяемые, помеченные “минусом”
неисправности - для них нельзя построить тестовые наборы! Для них будут
неприятности, перебор..
В качестве
совета: “много минусов” - косвенное свидетельство плохой реализации!
Затем по
эквивалентным кубическим покрытиям, построенным в л/р№.3 надо
спроектировать вручную тест для активизации каждого пути в значениях 0 и 1.
Этот тест достаточен для контроля одиночных константных существенных
неисправностей, что надо подтвердить методом моделирования неисправностей,
используя программу анализа полноты теста под названием F.bat. Если появились новые, помеченные “минусом”
неисправности, то, скорее всего, Вы где-то ошиблись в выкладках!
Прежде, чем
проектировать тест по кубическим покрытиям для комбинационной схемы, нужно
проверить тривиальный тест из 16 наборов (лабораторная работа №1) на полноту.
Для этого надо запустить программу F.bat и задать два параметра: первый – файл описания нашей
схемы (имя_схемы.cmp) и второй
- файл в который будет выведен результат работы. Командная строка для
нашего примера должна выглядеть следующим образом:
f.bat имя_схемы rezult
В конце файла,
в котором сохраняется результат, будет приведена таблица с результатом теста.
Проанализировав
таблицу, необходимо определить непроверяемые неисправности (если они имеются),
или убедиться в том, что непроверяемых неисправностей нет.
Известно, что
тривиальный тест (16 наборов) избыточен, поэтому необходимо вручную создать
свой тест, проверяющий те же неисправности, что и тест из 16 наборов.
Для
этого:
·
выпишите все кубы из без противоречий единичного и нулевого покрытия
(данные из л/р № 3 результат работы программы pialg);
·
сделайте проверку на неисправность в виде тождественного нуля или
единицы для каждого из входов. Проверка выполняется с помощью D
– пересечения над соответствующими кубами (см. Таблицу 4.1).
|
D
|
0
|
1
|
х
|
|
0
|
0
|
D
|
0
|
|
1
|
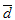
|
1
|
1
|
|
х
|
0
|
1
|
x
|
Таблица 4.1. D-пересечение.
·
выпишите полученные единичные и нулевые покрытия, исключив повторяющиеся
кубы.
Вот и получился
тестовый набор. Проверьте его, еще раз запустив
f.bat имя_схемы result
Также
необходимо привести удачную и неудачную попытки активизации (пути).
*** Анализ полноты по
внешним входам
|
Вход
|
1
|
2
|
3
|
4
|
|
Неиспр.
|
01
|
01
|
01
|
01
|
|
Проверка
|
++
|
++
|
++
|
++
|
*** Анализ полноты по элементам
|
Вход
|
1
|
2
|
3
|
4
|
5
|
6
|
Ou
|
|
Неиспр.
|
01
|
01
|
01
|
01
|
01
|
01
|
01
|
|
Элем. 1
|
-+
|
|
|
|
|
|
+-
|
|
Элем. 2
|
++
|
|
|
|
|
|
++
|
|
Элем. 3
|
+-
|
++
|
|
|
|
|
++
|
|
Элем. 4
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 5
|
++
|
|
|
|
|
|
++
|
|
Элем. 6
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 7
|
++
|
|
|
|
|
|
++
|
|
Элем. 8
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 9
|
++
|
|
|
|
|
|
++
|
|
Элем. 10
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 11
|
++
|
|
|
|
|
|
++
|
|
Элем. 12
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 13
|
++
|
|
|
|
|
|
++
|
|
Элем. 14
|
++
|
++
|
|
|
|
|
++
|
|
Элем. 15
|
++
|
++
|
|
|
|
|
++
|
По результатам
теста можно выявить следующие непроверяемые неисправности:
·
тождественный «0» на 1-м входе элемента 1;
·
тождественная «1» на 1-м входе элемента 2.
Нетрудно заметить
по схеме (л/р №1), что непроверяемая неисправность на входе 1го
элемента оказывает непосредственное влияние на 1й вход 3го
элемента.
Построим тест вручную.
Первый путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C7
|
1
|
x
|
x
|
0
|
1
|
x
|
x
|
x
|
x
|
1
|
|
C1
|
0
|
x
|
0
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
|
|
d
|
x
|
0
|
0
|
1
|
x
|
x
|
x
|
0
|
|
|
d = 1
|
1
|
x
|
0
|
0
|
1
|
x
|
x
|
x
|
0
|
1’
|
|
d = 0
|
0
|
x
|
0
|
0
|
1
|
x
|
x
|
x
|
0
|
0’
|
Наборы: 0101 1 и
0100 0
Второй путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
1
|
|
C’3
|
0
|
1
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
|
|
0
|
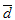
|
1
|
0
|
1
|
x
|
x
|
x
|
0
|
|
|
d = 1
|
0
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
0
|
1’
|
|
d = 0
|
0
|
1
|
1
|
0
|
1
|
x
|
x
|
x
|
0
|
0’
|
Наборы: 1100 1 и
110? 0 - противоречие
Третий путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
1
|
|
C1
|
0
|
x
|
0
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
|
|
0
|
0
|
d
|
0
|
1
|
х
|
х
|
х
|
х
|
|
|
d = 1
|
0
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
0
|
1’
|
|
d = 0
|
0
|
0
|
0
|
0
|
1
|
x
|
x
|
x
|
0
|
0’
|
Наборы: 1100 1 и
0100 0
Четвертый путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
1
|
|
C3
|
x
|
x
|
x
|
1
|
x
|
x
|
x
|
1
|
x
|
0
|
|
|
x
|
0
|
1
|
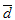
|
1
|
x
|
x
|
1
|
x
|
|
|
d = 1
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
1
|
x
|
1’
|
|
d = 0
|
x
|
0
|
1
|
1
|
1
|
x
|
x
|
1
|
x
|
0’
|
Наборы: 1100 1 и
1110 0
Пятый путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C8
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
x
|
1
|
|
C6
|
x
|
x
|
x
|
x
|
0
|
x
|
x
|
x
|
0
|
0
|
|
|
x
|
0
|
1
|
0
|
d
|
x
|
x
|
x
|
0
|
|
|
d = 1
|
x
|
0
|
1
|
0
|
1
|
x
|
x
|
x
|
0
|
1’
|
|
d = 0
|
x
|
0
|
1
|
0
|
0
|
x
|
x
|
x
|
0
|
0’
|
Наборы: 1100 1 и
1000 0
Шестой путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C9
|
x
|
x
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
1
|
|
C2
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
x
|
x
|
0
|
|
|
x
|
x
|
x
|
1
|
x
|
d
|
1
|
0
|
1
|
|
|
d = 1
|
x
|
x
|
x
|
1
|
x
|
1
|
1
|
0
|
1
|
1’
|
|
d = 0
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
0
|
1
|
0’
|
Наборы: 0111 1 и
0011 0
Седьмой путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C10
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
1
|
1
|
|
C2
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
x
|
x
|
0
|
|
|
x
|
x
|
x
|
1
|
x
|
0
|
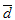
|
0
|
1
|
|
|
d = 1
|
x
|
x
|
x
|
1
|
x
|
0
|
0
|
0
|
1
|
1’
|
|
d = 0
|
x
|
x
|
x
|
1
|
x
|
0
|
1
|
0
|
1
|
0’
|
Наборы: 0110 1 и
0011 0
Восьмой путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C9
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
1
|
1
|
|
C3
|
x
|
x
|
x
|
1
|
x
|
x
|
x
|
1
|
x
|
0
|
|
|
x
|
x
|
x
|
1
|
x
|
x
|
0
|
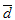
|
1
|
|
|
d = 1
|
x
|
x
|
x
|
1
|
x
|
x
|
0
|
0
|
1
|
1’
|
|
d = 0
|
x
|
x
|
x
|
1
|
x
|
x
|
0
|
1
|
1
|
0’
|
Наборы: 0x10 1 и
1x10 0
Девятый путь
|
|
20
|
20
|
17
|
19
|
18
|
18
|
20
|
17
|
19
|
|
|
C10
|
x
|
x
|
x
|
x
|
x
|
x
|
0
|
0
|
1
|
1
|
|
C6
|
x
|
x
|
x
|
x
|
0
|
x
|
x
|
x
|
0
|
0
|
|
|
x
|
x
|
x
|
x
|
0
|
x
|
0
|
0
|
d
|
|
|
d = 1
|
x
|
x
|
x
|
x
|
0
|
x
|
0
|
0
|
1
|
1’
|
|
d = 0
|
x
|
x
|
x
|
x
|
0
|
x
|
0
|
0
|
0
|
0’
|
Наборы: 0010 1
и 0000 0
Объединим
полученные кубы единичного и нулевого покрытия – это и будет наш тест, который
покрыл все возможные неисправности.
Примечание. При выписывании кубов, составляющих тест, будьте осторожны, исключая некоторые кубы из теста. В
данном случае нельзя проводить аналогию с
минимизацией булевых функций. Так как, Вы можете потерять
тестовые наборы и в результате не получить ничего хорошего.
В приведенном
примере исключены кубы: (0х10
и 1х10), хотя
на первый взгляд могло показаться, что их стоит оставить, а исключить кубы (0010 и 1110). Еще раз -
БУДЬТЕ ВНИМАТЕЛЬНЫ.
У нас
получилось 9 тестовых наборов:
0101 1
1100 1
0111 1
0010 1
0100 0
1110 0
1000 0
0011 0
0000 0
Запустив
снова программу f.bat,
проверив созданный нами тест из 9 наборов, удалось убедиться в том, что
созданным тестом удалось покрыть те же неисправности, что и тестом из 16
наборов.
Удачная попытка
активизации пути для любой неисправности с указанием промоделированных значений
для схемы с задуманной неисправностью

Неудачная попытка
активизации пути в схеме с непроверяемой неисправностью.
Тестовое обеспечение
и тестопригодное проектирование
Здесь Вы
исследуете тестопригодность и проектируете тесты, работая в Tw-CAD с более
сложной схемой, в которой 16-разрядный сдвиговый регистр является источником
сигналов для 3 экземпляров Вашей комбинационной схемы.
16-разрядный
сдвиговый регистр собран из четырех 4-х разрядных микросхем (ИС)155ИР1.
ИС 155ИР1-это универсальный регистр, который работает с данными в 2 режимах:
·
либо сдвигает данные последовательно поступающие с входа DL, по c1 (при
PE=0,c2=1)
·
либо параллельно заносит данные с четырех D-входов
микросхемы по c2 (при PE=1,c1=1).
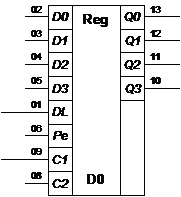
ИС 155ИР1
используется в исходной схеме только в режиме сдвига, из-за чего тесты
получаются длинными. На практике проблему длинных тестов, а главное непомерно
больших затрат на их проектирование решают добавлением оборудования для
упрощения тестирования. Представленные схемы достаточно просты, поэтому для них
проблематична только длина теста. Применимы 2 подхода, упрощающие
тестирование:
·
Ad-hoc–“изменения по месту” с минимумом дополнительного оборудования по
рекомендациям Tw-CAD. Ввиду единой структуры схемы в заданиях Tw-CAD
рекомендует единообразно для всех заданий точку дополнительного управления, как
бы разрезающую сдвиговый регистр на две части. Различие лишь в местоположении
точки в схемах по разным заданиям. Для реализации точки придетс
использовать микросхему 155ИР1 в полном объеме - как универсальный регистр. С
этой целью входы PE,c2,D рекомендованной к изменению ИС делают независимыми и
выносят на разъем, причем из 4 параллельных D-входов выносят на разъем только
один. Он соответствует разряду, на выходе которого рекомендовано ввести точку
дополнительного управления.
·
Согласно стандарту тестопригодного проектирования JTAG в режиме
тестирования схема разваливается на отдельные микросхемы, тестируемые
независимо друг от друга на заранее известных тестах этих микросхем (либо на
тестах, спроектированных отдельно для каждой микросхемы, как и предлагается
сделать в задании).
ОБЩИЕ РЕКОМЕНДАЦИИ.
•
Поместите схему, построенную ранее в библиотеку demo.bet с помощью Module из Tw-cad.bat
•
Создайте исходную (базовую схему) в
соответствии с номером варианта. Берем номер варианта в 10 системе исчисления,
переводим в четверичную и с левого края приписываем 3:
Вариант 2310
получим значение 1134 , допишем 3 (с
левого края) получим 3113.
ОПИСАНИЕ БАЗОВОЙ СХЕМЫ.
Таблица
использована для удобства описания подключения элементов S1, S2, S3.
Пояснения к
таблице:
·
Для элемента S2 подключение осуществляется
посредством перестановки симметрично середине 16-разрядного регистра.
·
Для элемента S3 подключение осуществляется
посредством перестановки симметрично середине секции.
|
№ по варианту
|
Элемент S1
|
Элемент S2
|
Элемент S3
|
Контакт
|
|
0
|
00
|
33
|
03
|
d
|
|
1
|
01
|
32
|
02
|
|
2
|
02
|
31
|
01
|
|
3
|
03
|
30
|
00
|
|
0
|
10
|
23
|
13
|
c
|
|
1
|
11
|
22
|
12
|
|
2
|
12
|
21
|
11
|
|
3
|
13
|
20
|
10
|
|
0
|
20
|
13
|
23
|
b
|
|
1
|
21
|
12
|
22
|
|
2
|
22
|
11
|
21
|
|
3
|
23
|
10
|
20
|
|
0
|
30
|
03
|
33
|
a
|
|
1
|
31
|
02
|
32
|
|
2
|
32
|
01
|
31
|
|
3
|
33
|
00
|
30
|
Полученное
значение: 3113
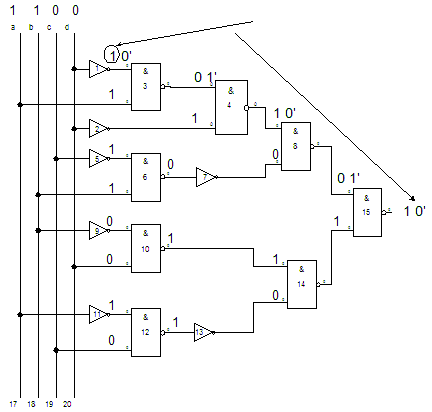
Базовая схема в
соответствии с номером варианта.
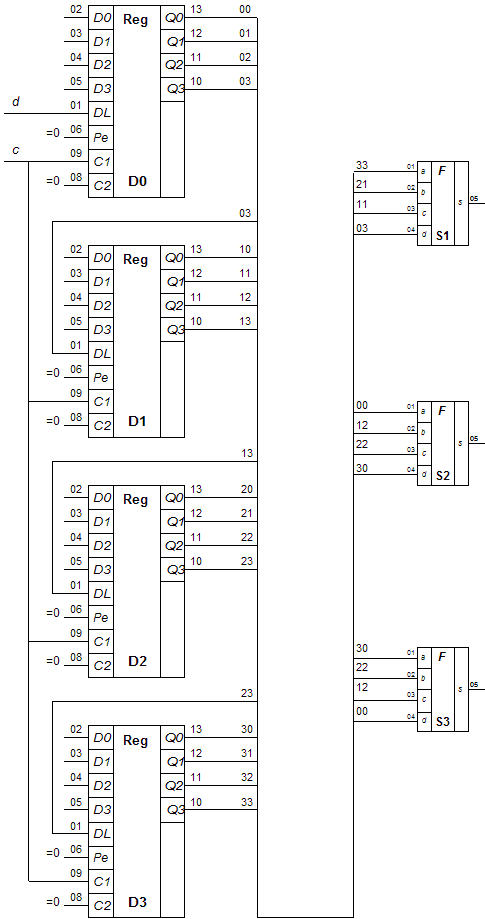
- S1, S2 и S3 – это три экземпляра нашей схемы
- D0, D1, D2, D3 – регистры, стандартные,
которые уже есть в библиотеке demo.bet.
- Каждый вход схем S1, S2, S3 нужно соединить с
соответствующим выходом от регистра, в соответствии с вариантом, пользуясь
таблицей
ОПИСАНИЕ МОДИФИЦИРОВАННЫХ СХЕМ.
1. Выполните
описание вашей базовой схемы и сохраните его в файле имя_схемы.rd1
2. Выполните
в TW-CAD программы:
• Modlsi
• Testable
• Test
3. После
выполнения каждой процедуры, найдите следующие данные:
- Оценки
управляемости и наблюдаемости (суммарные и максимальные); Шаг номер 35
работы Modlsi
-
Количество сегментов и тестовых наборов; Шаг номер 1 работы Test
-
Рассчитайте полноту теста;
РАСЧЕТ
ПОЛНОТЫ ТЕСТА.
Найдиет
следующие данные:
Шаг
номер 11 работы Test:
|
Схема:
|
|
Пример
|
|
Контактов модулей и разъемов
в схеме:
|
W
|
45
|
|
Проверенных константных
неисправностей:
|
X
|
71
|
|
Непроверенных константных
неисправностей:
|
Y
|
1
|
|
Непроверяемых константных
неисправностей:
|
Z
|
18
|
Полнота теста = ( (X +
Z) / W*2 ) * 100%
Полнота теста = ( (X +
Z) / W*2 ) * 100% = ( 89 / 90 )
*100% = 98,8%
4. Включите
полученные результаты в отчет.
5. Осуществив
рекомендации по улучшению, повторите шаги 1 - 4. Для этого вам необходимо
ознакомиться с реализацией ИС 155ИР1.Сохраните
модифицированную схему в соответствующем .rd1 файле (имя_схемы_3.rd1)
6. Измените
схему в стандарте JTAG, повторите шаги 1 - 4. Сохраните
модифицированную схему в соответствующем .rd1
файле (имя_схемы_4.rd1)
7. Проведите
сравнение трех полученных схем по:
•
оценкам управляемости и наблюдаемости;
•
качеству теста;
•
длине теста;
•
средней длине сегмента.
8. Опишите
схему с 16 выводами с регистров D0…D2
на дополнительный разъем. Повторите шаги 1-3. Сохраните модифицированную схему
в соответствующем .rd1 файле (имя_схемы_2.rd1)
9. Выполните
в TW-CAD программы:
·
Modlsi;
·
Outlib (введите кол-во сегментов
и имя файла, в котором хотите сохранить шапку теста). Тест будет состоять из
четырех сегментов. В каждом сегменте количество наборов определяется согласно
подключению схемы S2. Для тестирования выбран именно
этот элемент схемы
ПРОЕКТИРОВАНИЕ
ТЕСТА.
Итак,
созданная шапка теста:
1 0
*САПТ-ЛИТМО 0. 0
заполните эту форму LAB6_2
Разъемы :*I E T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ 1.
1*???????????????????????*
@ . 2
???????????????????????
Необходимо
привести тест к виду приведенному ниже, согласно вашей схеме, путем прогона
каждого из кубов заданного единичного покрытия с входов схемы, таким образом,
чтобы на соответствующих контактах получить требуемый результат (исходное
покрытие и «1» на контакте, соответствующем элементу S2). Переход на контакте «18»
(по схеме из примера – это сигнал С) должен быть с 0 на 1
(для реализации сдвига), поэтому необходимо менять значения только на
контакте «17» (по схеме из примера – это сигнал D).
Ниже представлен пример одного
сегмента теста для куба: x101
*САПТ-ЛИТМО 0. 0 заполните
эту форму LAB6_2
1
Разъемы :*I * E T
*
Разъемы :*N X
Контакты:*
Контакты:*11
Контакты:*78
@ 1. 1*11*
@ . 2 10
@ . 3*x1*
@ . 4 x0
@ . 5*01*
@ . 6 00
@ . 7*x1*
@ . 8 x0
@ . 9*x1*
@ . 10 x0
@ . 11*x1*
@ . 12 x0
@ . 13*11*
@ . 14 10
@ . 15*x1*
@ . 16 x0
@ . 17*x1*
@ . 18 x0
@ . 19*x1*
@ . 20 x0
@ . 21*x1*
@ . 22 x0
@ . 23*x1*
@ . 24 x0
@ . 25*x1*
@ . 26 x0
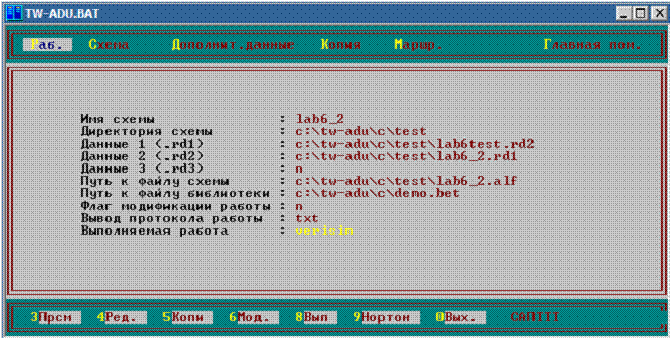
Создав файл с тестовым набором,
необходимо запустить программу verisim, как показано на рисунке ниже.
Здесь:
·
Данные 1: файл с тестом
·
Данные 2: файл с описанием схемы
ПРИМЕР.
Описание базовой схемы (lab6.rd1):
ПЛАТА: lab6;
155ир1 - D0: 01/d, 06/ре, 09/c1, 08/c2;
*: 13/00, 10/03;
155ир1 - D1: 01/03, 06/ре,
09/c1, 08/c2;
*: 12/11, 11/12, 10/13;
155ир1 - D2: 01/13, 06/ре,
09/c1, 08/c2;
*: 12/21,
11/22, 10/23;
155ир1 - D3: 01/23, 06/ре, 09/c1,
08/c2;
*: 13/30, 10/33;
lab2_1 - s1: 1/33, 2/21, 3/11,
4/03;
*: 5/s1;
lab2_1 - s2: 1/00, 2/12, 3/22,
4/30;
*: 5/s2;
lab2_1 - s3: 1/30, 2/22, 3/12,
4/00;
*: 5/s3;
КОЛОДКА - in:
1/d, 2/c1, 3/ре, 4/c2;
КОЛОДКА - ex:
5/s1, 6/s2, 7/s3;
f0: ре, c2;
Оценки управляемости и
наблюдаемости
Управляемость 100 % (sum 17392) (max 797)
Наблюдаемость 100 % (sum 11361) (max 202)
Полнота
(89/90)*100% = 98,8%
Тестопригодность 100 %
CEГMEHTOB
14
HAБOPOB
393
* * * * * * Рекомендации по улучшению
тестопригодности * * * * * *
* * * * *
* В а р и а н
т #
1 * * * * * *
|
Точка
доп.управления
|
Номер макро
|
Оценки
упавляемости
|
Схемное
обозначение
|
|
Суммарная
|
MAX
|
|
----- 1-----
|
26
|
9619
|
435
|
|
|
Источник сигнала
(прямого)
|
|
|
|
155ИР1-D2:12\134ИР1Т2-2:25;
|
|
Приемники
сигнала
(прямого)
|
11
|
|
|
134ИР1Т1-3:4;
|
|
|
26
|
|
|
y;
|
|
|
33
|
|
|
LAB2_1-S1:2\НЕИ-6:2;
|
|
|
33
|
|
|
LAB2_1-S1:2\НЕИ-9:1;
|
Минимально необходимые изменения
1.(0) Макро 26 Изменения по выбору
разработчика.
Вариант предполагает 0 дополнительных
входа/выхода на колодку
Максимальные разумные изменения
1.(C) Макро 26 Мультиплексор на входе
с независимым дополнительным входом
данных
Вариант предполагает 2 дополнительных
входа/выхода на колодку
Измененная по рекомендациям схема
(lab6_3.rd1):
ПЛАТА: lab6_3;
155ир1 - D0: 01/d, 06/ре, 09/c1, 08/c2;
*: 13/00, 10/03;
155ир1 - D1: 01/03, 06/ре, 09/c1, 08/c2;
*: 12/11, 11/12, 10/13;
155ир1 - D2: 01/13, 03/d2, 06/реD2, 09/c1, 08/c2D2;
*: 12/21, 11/22, 10/23;
155ир1 -
D3: 01/23, 06/ре, 09/c1, 08/c2;
*: 13/30, 10/33;
lab2_1 - s1: 1/33, 2/21, 3/11,
4/03;
*: 5/s1;
lab2_1 - s2: 1/00, 2/12, 3/22,
4/30;
*: 5/s2;
lab2_1 - s3: 1/30, 2/22, 3/12,
4/00;
*: 5/s3;
КОЛОДКА - in:
1/d, 2/c1, 3/ре, 4/d2, 5/реD2, 6/c2D2;
КОЛОДКА - ex:
7/s1, 8/s2, 9/s3;
f0: ре, c2;
Оценки управляемости и наблюдаемости
Управляемость 100 % (sum 11834) (max 621)
Наблюдаемость 100 % (sum 9667) (max 192)
Тестопригодность 100 %
Полнота
(90/90)*100% = 100%
CEГMEHTOB
18
HAБOPOB
472
Измененная по стандарту JTAG схема (lab6_4.rd1):
ПЛАТА: lab6_4;
155ир1 - D0: 01/d, 06/ре, 09/c1, 08/c2;
*: 13/00, 10/03;
155ир1 - D1: 01/03, 06/ре, 09/c1, 08/c2;
*: 12/11, 11/12, 10/13;
155ир1 - D2: 01/13, 06/ре, 09/c1, 08/c2;
*: 12/21, 11/22, 10/23;
155ир1 -
D3: 01/23, 06/ре, 09/c1, 08/c2;
*: 13/30, 10/33;
lab2_1 - s1: 1/33, 2/21, 3/11,
4/03;
*: 5/s1;
lab2_1 - s2: 1/00, 2/12, 3/22,
4/30;
*: 5/s2;
lab2_1 - s3: 1/30, 2/22, 3/12,
4/00;
*: 5/s3;
КОЛОДКА - in:
1/d, 2/c1, 3/ре, 4/c2;
КОЛОДКА - ex:
5/s1, 6/s2, 7/s3;
f0: ре, c2;
rt: 00, 03, 11, 12, 21, 22, 30, 33;
Оценки управляемости и наблюдаемости
Управляемость 100 % (sum 6558) (max 337)
Наблюдаемость 100 % (sum 241) (max 6)
Тестопригодность 100 %
Полнота
(90/90)*100% = 100%
CEГMEHTOB
30
HAБOPOB
228
Сравнительная характеристика схем lab6.rd1, lab6_3.rd1, lab6_4.rd1
|
|
Lab6.rd1
|
Lab6_3.rd1
|
Lab6_4.rd1
|
|
Управляемость
(суммарная / макс)
|
17392 / 797
|
11834 / 621
|
6558 / 337
|
|
Наблюдаемость
(суммарная / макс)
|
11361 / 202
|
9667 / 192
|
241 / 6
|
|
Полнота теста
|
98,8%
|
100%
|
100%
|
|
Длина теста,
наборов
|
393
|
472
|
228
|
|
Кол-во сегментов
|
14
|
18
|
30
|
|
Средняя длина теста
= (кол-во наборов/ число сегментов)
|
28
|
26,2
|
7,6
|
Как видно из приведенной
таблицы при переходе от схемы 1 к схеме 3:
- происходит улучшение
показателей управляемости и наблюдаемости;
- достигается 100% полнота теста;
- количество сегментов теста
растёт;
- средняя длина теста
сокращается, вместе с тем для схемы 2 общая длина теста оказывается
максимальной, а для схемы 3 – минимальной.
Измененная схема с выводом на
один разъем выходов D0…D2(lab6_2.rd1):
ПЛАТА: lab6_2;
155ир1 - D0: 01/d, 06/ре, 09/c1, 08/c2;
*: 13/00, 10/03, 11/02, 12/01;
155ир1 - D1: 01/03, 06/ре, 09/c1, 08/c2;
*: 12/11, 11/12, 10/13, 13/10;
155ир1 - D2: 01/13, 06/ре, 09/c1, 08/c2;
*:
12/21, 11/22, 10/23, 13/20;
155ир1 - D3: 01/23, 06/ре, 09/c1, 08/c2;
*: 13/30, 10/33, 12/31, 11/32;
lab2_1 - s1: 1/33,
2/21, 3/11, 4/03;
*: 5/s1;
lab2_1 - s2: 1/00,
2/12, 3/22, 4/30;
*: 5/s2;
lab2_1 - s3: 1/30,
2/22, 3/12, 4/00;
*: 5/s3;
КОЛОДКА - in: 17/d, 18/c1, 19/ре, 20/c2;
КОЛОДКА - ex: 21/s1, 22/s2, 23/s3;
f0: ре, c2;
КОЛОДКА - t: 1/00, 2/01, 3/02, 4/03;
*: 5/10, 6/11, 7/12, 8/13;
*: 9/20, 10/21, 11/22, 12/23;
*: 13/30, 14/31, 15/32, 16/33;
Тест из 4х сегментов (исходное единичное
покрытие).
1 4
*САПТ-ЛИТМО 0. 0 заполните
эту форму
LAB6_2
1
Разъемы :*I * E
T
*
Разъемы :*N
X
Контакты:*
Контакты:*11
Контакты:*78
@ 1. 1*11*
@ . 2 10
@ . 3*x1*
@ . 4 x0
@ . 5*01*
@ . 6 00
@ . 7*x1*
@ . 8 x0
@ . 9*x1*
@ . 10 x0
@ . 11*x1*
@ . 12 x0
@ . 13*11*
@ . 14 10
@ . 15*x1*
@ . 16 x0
@ . 17*x1*
@ . 18 x0
@ . 19*x1*
@ . 20 x0
@ . 21*01*
@ . 22 00
@ . 23*x1*
@ . 24 x0
@ . 25*x1*
@ . 26 x0
*САПТ-ЛИТМО 0. 0
заполните эту форму
LAB6_2
2
Разъемы :*I * E
T
*
Разъемы :*N
X
Контакты:*
Контакты:*11
Контакты:*78
@ 2. 1*x1*
@ . 2 x0
@ . 3*x1*
@ . 4 x0
@ . 5*11*
@ . 6 10
@ . 7*x1*
@ . 8 x0
@ . 9*x1*
@ . 10 x0
@ . 11*x1*
@ . 12 x0
@ . 13*11*
@ . 14 10
@ . 15*x1*
@ . 16 x0
@ . 17*x1*
@ . 18 x0
@ . 19*x1*
@ . 20 x0
@ . 21*01*
@ . 22 00
@ . 23*x1*
@ . 24 x0
@ . 25*01*
@ . 26 00
*САПТ-ЛИТМО 0. 0
заполните эту форму
LAB6_2
3
Разъемы :*I * E
T
*
Разъемы :*N
X
Контакты:*
Контакты:*11
Контакты:*78
@ 3. 1*01*
@ . 2 00
@ . 3*x1*
@ . 4 x0
@ . 5*01*
@ . 6 00
@ . 7*x1*
@ . 8 x0
@ . 9*x1*
@ . 10 x0
@ . 11*x1*
@ . 12 x0
@ . 13*11*
@ . 14 10
@ . 15*x1*
@ . 16 x0
@ . 17*x1*
@ . 18 x0
@ . 19*x1*
@ . 20 x0
@ . 21*01*
@ . 22 00
@ . 23*x1*
@ . 24 x0
@ . 25*11*
@ . 26 10
*САПТ-ЛИТМО 0. 0
заполните эту форму
LAB6_2
4
Разъемы :*I * E
T
*
Разъемы :*N
X
Контакты:*
Контакты:*11
Контакты:*78
@ 4. 1*01*
@ . 2 00
@ . 3*x1*
@ . 4 x0
@ . 5*11*
@ . 6 10
@ . 7*x1*
@ . 8 x0
@ . 9*x1*
@ . 10 x0
@ . 11*x1*
@ . 12 x0
@ . 13*x1*
@ . 14 x0
@ . 15*x1*
@ . 16 x0
@ . 17*x1*
@ . 18 x0
@ . 19*x1*
@ . 20 x0
@ . 21*01*
@ . 22 00
@ . 23*x1*
@ . 24 x0
@ . 25*01*
@ . 26 00
Результаты моделирования теста (verisim)
*САПТ-ЛИТМО
0.** TECT HE ЗABEPШEH
***
LAB6_2
1
Разъемы :*I
E
T
*
Разъемы :*N
X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ 1.
1*110Н...................*
@ . 2
100Н...Е...............
@ . 3
.10Н...Е...............
@ . 4
.00Н....Е..............
@ . 5
010Н....Е..............
@ . 6 000Н...Н.Е.............
@ . 7
.10Н...Н.Е.............
@ . 8
.00Н....Н.Е............
@ . 9
.10Н....Н.Е............
@ . 10
.00Н.....Н.Е...........
@ . 11
.10Н.....Н.Е...........
@ . 12
.00Н......Н.Е..........
@ . 13 110Н......Н.Е..........
@ . 14
100Н...Е...Н.Е.........
@ . 15
.10Н...Е...Н.Е.........
@ . 16
.00Н....Е...Н.Е........
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
***
LAB6_2
2
Разъемы :*I
E
T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 17
.10Н....Е...Н.Е........
@ . 18
.00Н.....Е...Н.Е.......
@ . 19
.10Н.....Е...Н.Е.......
@ . 20
.00Н......Е...Н.Е......
@ . 21 010Н......Е...Н.Е......
@ . 22
000Н...Н...Е...Н.Е.....
@ . 23
.10Н...Н...Е...Н.Е.....
@ . 24
.00Н....Н...Е...Н.Е....
@ . 25
.10Н....Н...Е...Н.Е....
@ . 26
.00Н.ЕН..Н...Е...Н.Е...
@ 2.
1*.10Н...................*
@ . 2 .00Н...................
@ . 3
.10Н...................
@ . 4
.00Н...................
@ . 5
110Н...................
@ . 6
100Н...Е...............
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
***
LAB6_2
3
Разъемы :*I
E T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 7
.10Н...Е...............
@ . 8
.00Н....Е..............
@ . 9
.10Н....Е..............
@ . 10
.00Н.....Е.............
@ . 11
.10Н.....Е.............
@ . 12
.00Н......Е............
@ . 13
110Н......Е............
@ . 14
100Н...Е...Е...........
@ . 15
.10Н...Е...Е...........
@ . 16
.00Н....Е...Е..........
@ . 17
.10Н....Е...Е..........
@ . 18
.00Н.....Е...Е.........
@ . 19
.10Н.....Е...Е.........
@ . 20
.00Н......Е...Е........
@ . 21
010Н......Е...Е........
@ . 22
000Н...Н...Е...Е.......
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
*** LAB6_2
4
Разъемы :*I
E
T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 23
.10Н...Н...Е...Е.......
@ . 24 .00Н....Н...Е...Е......
@ . 25
010Н....Н...Е...Е......
@ . 26
000Н.Е.Н.Н...Е...Е.....
@ 3.
1*010Н...................*
@ . 2
000Н...Н...............
@ . 3
.10Н...Н...............
@ . 4
.00Н....Н..............
@ . 5
010Н....Н..............
@ . 6
000Н...Н.Н.............
@ . 7
.10Н...Н.Н.............
@ . 8
.00Н....Н.Н............
@ . 9
.10Н....Н.Н............
@ . 10
.00Н.....Н.Н...........
@ . 11
.10Н.....Н.Н...........
@ . 12
.00Н......Н.Н..........
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
***
LAB6_2
5
Разъемы :*I
E
T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 13
110Н......Н.Н..........
@ . 14
100Н.Н.Е...Н.Н.........
@ . 15
.10Н.Н.Е...Н.Н.........
@ . 16
.00Н....Е...Н.Н........
@ . 17
.10Н....Е...Н.Н........
@ . 18
.00Н.....Е...Н.Н.......
@ . 19
.10Н.....Е...Н.Н.......
@ . 20 .00НН.....Е...Н.Н......
@ . 21
010НН.....Е...Н.Н......
@ . 22
000Н...Н...Е...Н.Н.....
@ . 23
.10Н...Н...Е...Н.Н.....
@ . 24
.00Н....Н...Е...Н.Н....
@ . 25
110Н....Н...Е...Н.Н....
@ . 26
100Н.ЕНЕ.Н...Е...Н.Н...
@ 4. 1*010Н...................*
@ . 2
000Н...Н...............
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
***
LAB6_2
6
Разъемы :*I
E
T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 3
.10Н...Н...............
@ . 4
.00Н....Н..............
@ . 5
110Н....Н..............
@ . 6
100Н...Е.Н.............
@ . 7
.10Н...Е.Н.............
@ . 8 .00Н....Е.Н............
@ . 9
.10Н....Е.Н............
@ . 10
.00Н.....Е.Н...........
@ . 11
.10Н.....Е.Н...........
@ . 12
.00Н......Е.Н..........
@ . 13
.10Н......Е.Н..........
@ . 14
.00Н.......Е.Н.........
@ . 15
.10Н.......Е.Н.........
@ . 16
.00Н........Е.Н........
@ . 17
.10Н........Е.Н........
@ . 18
.00Н.........Е.Н.......
*САПТ-ЛИТМО 0.** TECT HE ЗABEPШEH
*** LAB6_2
Разъемы :*I
E
T
*
Разъемы :*N X
Контакты:*
Контакты:*1112222
1111111
Контакты:*78901231234567890123456
@ . 19
.10Н.........Е.Н.......
@ . 20
.00Н..........Е.Н......
@ . 21
010Н..........Е.Н......
@ . 22
000Н...Н.......Е.Н.....
@ . 23
.10Н...Н.......Е.Н.....
@ . 24
.00Н....Н.......Е.Н....
@ . 25
010Н....Н.......Е.Н....
@ . 26
000Н.Е.Н.Н.......Е.Н...
ИТОГО ***
для СХЕМЫ LAB6_2
ИТОГО смоделиpовано 62
значений ( 77%)
ИТОГО из
возможных 80 значений
Y:
1.z, 2.z, 3.z, 4.z, 5.z,
6.z, 7.z, 8.z, 9.z, 10.z
Y: 11.z,
12.z, 13.z, 17.z, 18.z, 19.z, 20.z, 21.z, 22.z, 23.z
Y:
24.z, 25.z, 26.z, 27.z, 28.z, 29.z,
Z:
33.0, 34.z, 35.0,
X:
49.z, 50.z, 51.0, 52.1,
ИТОГО
BCEГO CEГMEHTOB 4
ИТОГО
BCEГO HAБOPOB 104
ИТОГО
BPEMЯ CИHTEЗA TECTA 0
Mинут
ÓCompiled by Ignatiev N.O.
26.06.04