Лекции 1, 2,3
3 вида формул в
математике - 3 вида выражений в Фортране
2 вида формул в математике – это числовые,
логические.
3 вида выражений в Фортране – это
числовые, логические, строковые.
Числовые формулы - арифметические
выражения
Константы и переменные
Функции
в Фортране
Операции над числами
Оператор
присваивания
Логические выражения и логический
оператор присваивания
Логический оператор
присваивания
Отношения
Логические операции
Старшинство операций при вычислении логических
выражений
Булева алгебра и ее
интерпретации
Заключительные примеры
Обработка строк - строковые
выражения
Строковые константы, переменные и подстроки
Стандартные функции обработки
строк
Строковое выражение и
строковый оператор присваивания
Заключительные замечания и
примеры
Числовые
формулы - арифметические выражения
Осмысленная математическая формула,
записанная по правилам Фортрана, называется арифметическим выражением.
Правила записи выражений - это компромисс между способом, привычным для
математика и способом, возможным для компьютера.
По сравнению с Фортраном
- способ написания формул в других языках
программирования и электронных таблицах ничем принципиально не отличается
- заметно различается лишь список имен функций
- текстовый редактор WORD и MathCAD имеют средства
отображения формул, близкие к способу, принятому в математике. В них
используются специализированные редакторы формул, тогда как в языках
программирования для подготовки формул используют стандартные текстовые
редакторы
- в пакете "DERIVE" для аналитических
манипуляций с формулами их набирают в форме, похожей на языки
программирования, отображают на экране в форме, близкой к математической и
трансформируют в текст как для программ на "Fortran",
"Pascal" и "C".
Основная идея записи формул в языках программирования - превратить
любую витиеватую многоэтажную математическую формулу в строку символов,
пусть даже длинную. По известным правилам переноса ее можно записать в
нескольких последовательных строках бланка. Необходимость записывать формулы в
строку обусловлена тем, что компиляторы вводят формулы
последовательно символ за символом, как с клавиатуры. Основные принципы
записи формулы в виде арифметического выражения развивают указанную идею
и состоят в следующем:
• оформить формулу как длинную строку
символов
• именовать все величины по смыслу, а не обозначать
• единообразно именовать, а не обозначать функции
• единообразно писать операции, скобки ( в Фортране - только круглые скобки)
• иметь в виду тот же тип результата операции, что и тип операндов - это
соответствует тому, что в системе команд компьютера есть два разных комплекта
команд - для целых чисел и для вещественных чисел, но нет команд со смешанными
операндами
• иметь в виду, что результат вычисления выражения или его части с однотипными
операндами лежит том же классе чисел
• иметь в виду, что результат вычисления любого смешанного выражения или его части
всегда в самом широком классе чисел по отношению к операндам (самый узкий -
целые, шире - вещественные, еще шире - комплексные числа)
|
Принято
в математике
|
возможно
для компьютера
|
в
арифметическом выражении используют
|
|
Писать
многоэтажные формулы
|
вводить
данные
последовательно
|
Запись
формулы в строку любой длины
|
|
Использовать
разнообразные значки функций
Например
"знак квадратного корня"
|
нет
столько клавиш - надо использовать
при вводе только клавиши клавиатуры
|
Единообразие
по форме
F(x,y,..)
Где F-имя функции
Например sqrt(x) для квадратного
корня
|
|
обозначать величины буквами латинского, греческого,
древне-еврейского и других алфавитов
|
применять
только английские буквы a..z A..Z
|
Именовать величины по смыслу задачи;
|
|
обозначать индексы буквами i j k l m n
|
индекс
- это тоже имя
|
Часто
имена целых величин начинают
с букв I J K L M N
|
|
индексы
пишут снизу как Ak
|
пишут
в строку
|
A(k)
- в скобках - индекс
|
|
показатель
степени пишут сверху ab
|
пишут
в строку
|
a**b
|
|
деление
как a/b a : b
a
--
b
|
делают
единообразно и пишут в строку
|
a/b
|
|
умножение
как a· b ab AxB
|
пишут
единообразно
|
a*b
(нельз опускать * )
|
|
разные
скобки { } [ ] ( )
|
пишут
единообразно
|
( )
– только круглые
|
|
Тип
выражения
Real
Integer Complex
определяется
по смыслу задачи
|
тип результата тот же, что и тип операндов
|
Тип
подвыражения определяется автоматически – по самому широкому классу
операндов. Например 1/2 – это целая часть частного, то есть 0; однако
1./2=1/2.=1./2.=0.5
|
ИМЕНА
- имя
мнемонически передает смысл объекта
- имя
переменной, константы, функции, массива и другие имена состоят из
английских букв a..z, A..Z, цифр 0..9 и знаков “_” “$”
- имя
начинается с буквы
- в
имени допускается до 31 символа
- большие
и малые буквы в именах на языках "Fortran" и
"Pascal" не различаются
- в
языке "C" различаются большие и малые буквы в именах
- в
имени нельзя использовать пробелы- чаще всего его заменяют знаком
“_”
- в
имени нельзя использовать русские буквы - для них используют
транслитерацию
- например, Dlina_okrugnosti,
lenth_of_circle, speed, velocity, printer, A2
Отметим, что в Фортране в отличие от С и
Паскаль нет зарезервированных ключевых слов. Принята другая, более мягкая концепция
- по именам не должно быть двусмысленности, как в примере real x,y,max;
max=max(x,y) , где слева от "=" max - это простая переменная, а
справа от "=" max - это стандартная функция, вычисляющая максимум.
Константы и переменные
Фортран - это переводчик математических
формул. В формулы входят константы, переменные, векторы, матрицы и их
компоненты, над которыми выполняются какие-либо действия. Поэтому, как и в
математике в языках программирования появились такие объекты.
Константа - это неизменная величина, которой приписано
определенное значение. Как и в математике, имеются явные и именованные
константы
·
например, -18 и 1.25 - это явные
константы
·
обратите внимание, что вслед за
американцами, придумавшими Фортран, мы теперь тоже будем писать десятичную
"точку", а не "запятую"
·
как и в математике, очень большие и
очень маленькие вещественные числа записываются в экспоненциальной форме с указанием мантиссы и порядка.
Например, 0.0000015 легче читается, если ее записать как
0.15 10-5. В фортране принято писать 0.15e-5, где основание 10
обозначено буквой e, а десятичный порядок вместе со знаком "минус"
опущены из показателя вровень с буквой e. Обратите внимание, что никакого знака
умножения в записи константы нет и быть не может.
·
по внешнему виду явные константы
различают по типу - целые пишутся без десятичной точки,
·
например, -127 - это целая
константа, в то же время -127.
+25.871 0.0294, 0.15e-5 - это вещественные константы
- обязательно пишутся с десятичной точкой, независимо от того есть ли у числа
дробная часть или нет.
Указание типа важно для выбора подходящего
набора команд компьютера - вещественные и целые по-разному представляются в
компьютере, и даже одни и те же математические операции выполняются с помощью
разных команд компьютера. Математические операции над целыми и вещественными
числами выполняются в компьютере по-разному
·
с целыми безошибочно, но в более узком
диапазоне чисел
·
с вещественными чаще всего с
погрешностями, но в более широком диапазоне
·
со смешанными операндами - с
предварительным автоматическим переводом в самый широкий класс и диапазон чисел
по отношению к операндам
Для определения именованных констант имеется
специальный оператор parameter
(в отличие от математики никакие константы не подразумеваются - их нужно
определить). Например, используя оператор parameter( PI=3.1415928 ) определим константу PI - в
этом операторе через запятую можно определить и несколько констант:
integer KLON
! KLON-целая
real PI ,e !
PI-вещественная
complex
COMPL_DS ! COMPL_DS-комплексная
PARAMETER ( KLON=12 ,
COMPL_DS=(1.2,-8.5), PI=3.14159 , e=2.71)
в данном случае определены 3 числовые
константы, соответственно, KLON-целая, PI-вещественная, COMPL_DS-комплексная.
Комплексная константа COMPL_DS имеет мнимую часть 1.2 и
вещественную часть -8.5, заключенные в скобки.
В стиле Ф-90 лучше переписать так
integer, PARAMETER :: KLON=12
! KLON-целая константа
real , PARAMETER :: PI =3.14159 ,
e=2.71 ! e,PI -
вещественные константы
complex, PARAMETER ::
COMPL_DS=(1.2,-8.5) ! COMPL_DS - комплексная константа
Как видно из примеров, в Фортране предусмотрены все известные из математики
типы числовых величин - целые, вещественные и комплексные.
Для обеспечения строгого контроля над
описанием типов объектов указанный пример можно дополнить и написать так:
program
check_definitions
IMPLICIT NONE
integer, PARAMETER ::
KLON=12 ! KLON-целая
real , PARAMETER :: PI
=3.14159 ! PI-вещественная
complex, PARAMETER ::
COMPL_DS=(1.2,-8.5) ! COMPL_DS-комплексная
Переменная
·
величина, которая может изменяться в
программе
·
обязательно имеет собственное уникальное
имя
·
является скаляром
·
различается по написанию
o
простая переменная gamma
o
переменная с индексами al(2,3)
·
должна быть отнесена, как и именованная
константа
o
к одному из 5 базовых типов
§
integer - целые,
например, integer :: Ls=12, t1, gamma
§
real - вещественные, например, real
fe, PI, track
§
complex - комплексные, например, complex
COMPL_DS,c
- logical - логические, например, logical mumu,tomu
- character - строковые, например, character
stringer,coocker
- или к производному типу (ниже в примере my_type),
определяемому программистом
- type (my_type) my_type_var – это один из собственных типов, количество которых не
ограничено, а само его определение для простоты не приводится
Пример программы, вычисляющей по
заданной формуле
Имя константы, переменной, функции,
программы должно нести смысловую нагрузку, так, например, при вычислении длины
окружности по заданному радиусу программа может быть такой:
! Фамилия И.О., группа 121, вариант 1, лаба 1, дата 03.09.95 - чье и что это
prorgam
Dlina_okrugnosti
implicit
none
real,parameter
:: PI=3.14159
real dlina, radius
namelist /out/
radius,dlina ! перечень выводимых величин
write(*,*) '
введи radius= '
read(*,*) radius
! это чтение радиуса с консоли
dlina = 2. * PI * radius ! это длина окружности
write(*,out) !
это вывод на консоль переменных по перечню
end prorgam
Dlina_okrugnosti
Интересно, что достаточно изменить строку описания real dlina, radius
на строку описания real,dimension(1:5) :: dlina, radius
и программа будет считать, что dlina и radius - векторы, каждый по 5 чисел, и
потому неизменные по форме ввод, расчет и вывод будут выполнены для 5 чисел
вместо одного. Конечно, придется изменить данные с одного числа 2.8 на вектор
из 5 чисел 2.8, 7.2, 3., 12.1, 6.3
Векторы, матрицы относятся к массивам, которые более подробно рассматриваются позже.
Компилятор по умолчанию
(что не рекомендуется позволять) сам относит те или иные величины к целому либо
вещественному типу по первой букве в имени:
·
рекомендуется
использовать IMPLICIT NONE
- тогда компилятор сообщит обо всех величинах, для которых тип явно не указан
·
IMPLICIT
NONE
заставляет от задания типа по первой букве отказаться и явно описывать типы
величин, чтобы избежать возможных недоразумений
·
по умолчанию
o
компилятор относит к
целым (integer), если 1-ая буква в имени I,J,K,L,M,N , например, IGLA,
o
компилятор относит к
вещественным (real), если 1-ая буква в имени не I,J,K,L,M,N,
например GLASS.
o
для комплексных,
логических и строковых величин, правила выбора типа по первой букве вообще нет
Помимо числовых констант в Фортране
допустимы:
- строковые (текстовые) константы, они уже встречались в примерах - это
любой текст, заключенный в апострофы; например, ' введи radius= '
- логические константы .TRUE. .FALSE.
Более полно все возможные типы величин будут
рассмотрены позднее.
Функции в Фортране
Многочисленных значков функций, широко используемых при записи
формул в математике, нет на клавиатуре компьютера. Чтобы преодолеть это затруднение,
форма записи функций в компьютере по аналогии с F(x,y) из
математики унифицирована: имя( x,y,.. ) , где имя
- это имя, начинающееся с буквы, x,y,.. - это аргументы функции. Каждой функции
сопоставлено мнемоническое имя, максимально похожее на используемое в
математике, а список имен стандартных функций имеется в помощи по языку. В
стандарте Фортрана перечислено более сотни самых разнообразных стандартных
функций, для примера укажем некоторые:
·
алгебраические abs(x)
sqrt(x) min(a,b) max(a,b) mod(n,k)
·
тригонометрические sin(x) cos(x)
tan(x) atan(x)) с углом в радианах
·
и они же с углом в градусах sind(x)
cosd(x) tand(x) atand(x)
В руководстве по Фортрану и в помощи по
Фортрану имеется полный перечень стандартных функций, их параметры и
примеры применения
·
в Developer Studio для Windows и DOS
можно обратиться за помощью через оглавление помощи, либо получить контекстную
помощь, нажав F1, когда курсор внутри набранного имени функции
·
для DOS (ее в DOS вызывают единожды по
команде h в начале работы, а затем используют по Shft^F1
в любое время)
·
такая же форма записи функций ( только
со своими именами) используется программистом и при вызове своих
собственных функций.
·
обратите внимание, что нельзя писать без
скобок аргумент функции, как иногда делают в математике. Нельзя скобки
опускать, даже когда совсем нет аргументов.
В стандарте Фортрана
·
каждой из перечисленных стандартных
функций приписан тот или иной тип, например, sin(x) - вещественная
функция вещественного аргумента в радианах, sind(x) - вещественная
функция вещественного аргумента в градусах, mod(i,k) - целая функция
целого аргумента.
·
Для числовых функций действует понятие родовых имен по правилу: "тип
функции повторяет тип аргумента". Например, и получим разный тип для одной
и той же функции:
o
REAL - вещественный для abs(x) для real x
o
integer-целый для abs( k) для integer k
·
Функции преобразования типа не являются родовыми - их название
указывает, в какой тип преобразовать аргумент,
integer k
! целого типа число k
real
y ! вещественное число y
y=real(k) !
функция преобразования целого типа числа k в вещественное число real(k)
·
Как и в математике, для некоторых
функций допускается любое количество аргументов, например, max(a,b) и max(a,b,c)
одинаково допустимы.
Операции над числами
Все алгебраические операции над числами
представлены в Фортране:
|
в математике
|
операции
над числами
|
в Фортране
|
|
- a
|
противоположна величина
|
-a
|
|
a+b
|
сумма
|
a+b
|
|
a-b
|
разность
|
a-b
|
|
a·
b ab AxB
|
умножение
|
a*b
|
|
a a : b a/b
b
|
деление
|
a/b
при integer a,b дробь a/b определяется
как целая часть частного
|
|
ab
|
возведение в степень
|
a**b ,
1) для real a допустимо a>0
2 ) для integer b понимается как многократное умножение
|
Примечания:
• операции над комплексными числами выполняются
по соответствующим правилам, известным из математики
• для умножения и для деления допустим только один вариант записи операции:
деление, и возведение в степень вытянуты в строку
• никакие знаки операций (в частности умножение "*" ) в отличие от
математики нельзя опускать!
• операции над смешанными операндами выполняются с автоматическим
преобразованием всех операндов в наиболее широкий класс чисел по отношению к
операндам
Для формулы без скобок принят такой же, что
и в математике порядок выполнения операций:
- вычисление функций
- смена знака числа
- возведение в степень
- умножение и деление
- сложение и вычитание
Операции одного ранга в отсутствие скобок
("умножение и деление" либо "сложение и вычитание") выполняются
слева направо, несколько возведений в степень - наоборот справа налево. Как и в
математике, порядок выполнени операций можно изменить при помощи скобок, но в
отличие от математики допускаются только круглые скобки.
В основных языках программирования, как и в
математике, предусмотрены следующие типы числовых величин
|
Тип в
математике
|
Фортран
|
C
|
|
целые
|
integer он же integer*4
либо integer*2
либо integer*1
|
long либо short
либо int как long для Windows
либо int как short для DOS
|
|
вещественные
|
real или
double precision
|
float либо
double
|
|
комплексные
|
complex
|
нет такого
|
Имеется существенное различие между
числовыми множествами в математике и в Фортране:
·
в математике - числовые множества
бесконечны, а операции над числами, в принципе, можно выполнить точно; в
компьютере (в том числе и в Фортране) - диапазоны чисел ограниченны,
а множества чисел - конечны
·
только для целых чисел из допустимого диапазона операции над числами
можно выполнить точно
·
для вещественных чисел и диапазон чисел
ограничен, и сами числа представлены в памяти компьютера неточно и операции
над числами выполняются с ошибками округления;
·
поэтому при массовых вычислениях следует
исключать появление в промежуточных вычислениях малых чисел -
первоисточника ошибок округления (пример - вычитание близких по величине
чисел);
·
с помощью эквивалентных преобразований
получают формулы, которые исключают причины возникновения ошибок
округления
·
если все операнды одного типа, то и
результат этого же типа; обычно аргумент того же типа, что и функция, кроме
функций преобразования типов
·
числовая переменные, константы,
функции, входящие в арифметическое выражение, могут быть разного
типа; тип выполняемых операций над числами выбирается автоматически; тип
арифметического выражения и любого подвыражения (а также набор команд - целая,
вещественная или комплексная арифметика) выбирается автоматически по типам
операндов, вступающим в операции
·
если не все операндны одного типа, то
результат относится к самому широкому классу чисел; операнды автоматически
переводятся в самый широкий класс; классы чисел расширяются по типам так
же, как и в математике integer
==> real==>complex, а с учетом разновидностей
более подробно
integer*1==> integer*2 ==> integer*4 ==>real*4==>real*8==>complex*8==>complex*16
Обратные операции в математике, такие как
деление и извлечение корня могут выводить в более широкий класс чисел.
Например, в математике, если 1-целое, 2-целое, то 1 / 2 = 0.5 - вещественное;
например, если -4.0 - вещественное, то квадратный корень из -4 -
комплексное. В то же время в компьютере результат всегда относится к тому же
самому типу, что и операнды, и это следует понимать так:
- целое ** целое и вещественное**целое -понимают как
многократное умножение
- целое**вещественное и
вещественное** вещественное выполняют через
логарифмирование и потенцирование (отсюда основание степени -
неотрицательное)
- квадратнй корень sqrt(4.) - дает верный
результат 2.
- квадратнй корень sqrt(4) - дает неверный
результат или ошибку при компиляции, так как аргумент для
вещественной функции sqrt
должен быть вещественным
- квадратнй корень sqrt(-4.) - вызывает
ошибку (domain error) при выполнении, так как для вещественной
функции sqrt(x)
аргумент x не должен быть отрицательным
- квадратнй корень csqrt( (-4.,0.0) ) -
дает верный результат ( 0.0, 2.) - комплексный корень сsqrt(x) из комплексной
константы
- комплексный квадратнй корень csqrt(-4.) - дает ошибку
при компиляции, так как аргумент для комплексной функции csqrt должен быть
комплексным
- если возникает необходимость, программист должен
отслеживать эти особенности, расставляя точки в константах, используя
соответствующие функции более широкого класса чисел и пользуясь функциями
преобразования типов, см. помощь
Пример 1. 1-целое, 2-целое, а 1/2 => 0 -
целое - это целая часть частного,
но 1. / 2. => 0.5 - вещественное.
Пример 2. 9 ** ( 1 / 2) => 9**0 => 1 - целое.
Пример 3. 9. ** ( 1 / 2) => 9**0 => 1. -
вещественное.
Пример 4. 9**( 1. / 2) = =9**( 1 / 2. ) == 9**( 1. / 2. ) => 9**0.5 => 3. -
вещественное.
Пример 5. SQRT( - 4.) из-за отрицательного числа под корнем
использовать нельзя, так же как недопустимо и (-9.0)**2.0 , в то время как
(-9)**2 и (-9.0)**2 вполне допустимы.
Пример 6. 6 / 2 => 3 - целое, но 3.6 / 1.2 => 3. -
вещественное.
Типичные двусмысленности в написании
арифметических выражений приведены в методичке Практикум
по информатике, раздел
14.1
Из сказанного следует, что вычислению по
формулам должна предшествовать, кропотлива работа по нахождению ОДЗ - области
допустимых значений аргументов и еще более кропотливая работа по выявлению
диапазонов, где какая-либо часть формулы становится близкой к нулю, порождая
ошибки округления. Что совсем непривычно для математика - в разных дипазонах
можно отдавать предпочтение разным, эквивалетным с точки зрения алгебры
формулам, но имеющим разное поведение в смысле ошибок округления.
Где используются арифметические
выражения
Из всех видов выражений арифметические
выражения используются наиболее широко
• в арифметическом операторе присваивания
• в качестве аргументов функций и процедур
• в индексном выражении, при задании размерности массивов и при адресации
массивов и строк
• в константном выражении при инициализации
• как элемент списка вывода
• косвенно в логическом выражении при задании левой и правой частей отношений
• косвенно в строковом выражении при задании индексов
• вообще в каждом языке программирования и в электронных таблицах, наподобие
EXCEL
Лабораторная работа 1
Логические выражения и
логический оператор присваивания
Осмысленная логическая формула,
изучаемая в математической логике и записанная по правилам
Фортрана, называется логическим выражением. Принципы написания логических
выражений те же, что и для числовых формул
- вытянуть формулу в строку символов
- именовать по смыслу все величины, а не обозначать буквами разнообразных
алфавитов
- писать единообразно знаки функций,
операции, скобки
- имеются аналогии в сопоставлении
- логического и обычного умножения,
- логического и обычного сложения,
- логического и обычного отрицания
- для лучшего понимания полезно сопоставлять
понятия алгебры логики и обычной алгебры
В математической логике имеют
дело с истинностью высказываний, число “1” интерпретируют как TRUE
- истину, а число “0” как FALSE- ложь. Именно эти
слова, окруженные точками, выбраны в качестве логических констант в ФОРТРАНе.
Операндами в логической формуле являются логические переменные, отношения и
подвыражения, каждое из которых принимает одно из двух указанных значений. Значение
кодируется в компьютере одним битом из 4, 2 или 1 байтов. Логические
переменные и логические именованные константы надо описывать
в операторе описания типа, например
Logical L2,
h4; Logical, Parameter ::On=.TRUE.
В логическое выражение входят
·
логические константы,
·
логические переменные,
·
возможно использование, как встроенных
логических функций, так и логических функций, определяемых самим
программистом
·
отношения
·
логические операции
·
скобки, изменяющие порядок действий
Логические выражения используются
- в логическом операторе присваивания
- при инициализации
- как элемент списка вывода
- для записи условий в операторах IF, DO и WHERE
- вообще в каждом языке программирования и в
электронных таблицах, наподобие EXCEL
- в качестве аргументов функций и процедур
Логический
оператор присваивания
Логические переменные могут получать
значения в логическом операторе присваивания:
логическая_переменная
= логическое_выражение
Например Logical L2, h4;
Logical, Parameter ::On
= .TRUE.
h4 = On;
L2 = .FALSE.
В отличие от арифметического выражения, логическое
выражение никогда не бывает смешанным. В то же время
арифметические выражения могут быть левой и правой частью отношения, как и
строковые выражения. Отношение - это одна из составных частей логического
выражения.
Отношения.
Из всех перечисленных составных частей
наиболее просто понять назначение, смысл и написание отношений. Отношение - это
результат сравнения, например
·
- истинный .true.
·
-2>0
ложный .false.
|
В математике
|
Отношение
по-русски
|
По-английски
|
в Ф-77
|
в Ф-90
|
в языке С
|
|
f=g
|
"равно"
|
Equil
|
f .eq. g
|
f = =. g
|
f = = g
|
|
f#g
|
"не
равно"
|
No equil
|
f .ne.g
|
f /=g
|
f !=g
|
|
f< g
|
"меньше
чем"
|
Less than
|
f . lt. g
|
f < g
|
f < g
|
|
f> g
|
"больше
чем"
|
Great than
|
f . gt. g
|
f > g
|
f > g
|
|
f < = g
|
"меньше или
равно"
|
Less and equil
|
f . le. g
|
f <= g
|
f <= g
|
|
f > = g
|
"больше или
равно"
|
Great and equil
|
f .ge. g
|
f >= g
|
f >= g
|
выше, выражения f и g либо оба арифметические,
либо оба строковые. Каждое отношение после вычисления левой и правой частей
отношения принимает значение "истина" либо "ложь".
Например:
·
при
a=0 для отношения a+2 >= 3 получим 0+2 = 2 и
тогда 2> = 3 - это "ложь" или .false.
·
при a=3
получим 3+2 = 5 и тогда 5>= 3 - это"истина" или .true.
Логические
операции
Булева алгебра получила широкое применение в
математике, в вычислительной технике, в программировании и в системах
управления базами данных и т.д. Достаточно понятное толкование получают законы
булевой алгебры в так называемом исчислении высказываний, где в
качестве основных операций выступают союзы "ИЛИ" (дизьюнкция),
"И" (коньюнкция), "НЕ" (отрицание), используемые
практически в общепринятом смысле:
|
по-русски
|
по-английски
|
ФОРТРАН
|
в матлогике
|
аналог в алгебре
|
в языке
"C"
|
в языке
"Pascal"
|
|
ИЛИ
|
OR
|
a .OR. b
|
a+ b дизьюнкция
|
a+b сложение
|
a||b
|
a OR b
|
|
И
|
AND
|
a .AND. b
|
a&b коньюнкция
|
ab a.b умножение
|
a&&b
|
a AND b
|
|
НЕ
|
NOT
|
.NOT. a
|
~ a отрицание или инверсное значение
|
-a противоположная величина
|
!a
|
NOT a
|
Примечания:
·
ИЛИ следует понимать не как “либо -
либо”, а как не исключающее "ИЛИ"
·
в Pascal
в отличие от ФОРТРАН не
требуется окружать слова OR AND NOT точками,
потому что эти слова нельзя использовать в другом смысле
Пример. Определим переменную p00 как "точка
(x,y) - это начало координат" , тогда можно записать
integer x , y;
Logical p00
p00 = x .eq. 0 .and. y.eq. 0
Логическое выражение x .eq. 0 .and.
y.eq. 0 (высказывание о начале координат) можно прочитать так :
" x равно нулю И y равно нулю ". Затем выражение можно вычислить при различных X и Y
·
при x=0, y=1 -
ответ p00 = .false. , подробнее -
(0 равно 0 - это"истина") И (y равно 0 -
это"ложь"), "истина" И
"ложь" - это "ложь"; ответ "ложь"
·
при x=0, y=0 - ответ p00=.true.
, подробнее - получим (0 равно 0 - это "истина") И (0 равно
0 - это "истина"), "истина" И "истина"- это
"истина"; ответ "истина"
Запишем таблицы истинности логических
базовых операций наподобие привычной таблицы умножения в
приняв .false. - это
0 .true. - это 1
|
|
b=.false.
|
b=.true.
|
|
|
b=.false.
|
b=.true.
|
|
|
|
|
a=.false.
|
.false.
|
.false.
|
|
a=.false.
|
.false.
|
.true.
|
|
a=.false.
|
.true.
|
|
a=.true.
|
.false.
|
.true.
|
|
a=.true.
|
.true.
|
.true.
|
|
a=.true.
|
.false.
|
|
a&b a.and.b
|
|
a+b a.or.b
|
|
~a .not.a
|
У названных операций просматриваются
аналогии с обычными арифметическими операциями, в Фортране
·
a.and.b -
это логическое умножение
a&b 0*0=0 0*1=1 1*0=0
1*1=1
·
a.or.b - это логическое сложение a+ b 0+0=0
0+1=1 1+0=1 1+1=1
·
.not.a -
это логическое отрицание ~ a ~0=1 ~1=0
В Фортране-77 для удобства записи формул
добавлены две производные операции:
|
эквивалентность
|
и
|
неэквивалентность
|
|
|
b=.false.
|
B=.true.
|
|
|
b=.false.
|
b=.true.
|
|
a=.false.
|
.true.
|
.false.
|
|
a=.false.
|
.false.
|
.true.
|
|
a=.true.
|
.false.
|
.true.
|
|
a=.true.
|
.true.
|
.false.
|
|
A .eqv. b
.not.a.and..not.b .or. a.and.b
|
|
a .neqv. b
.not.(A
.eqv. b)
|
Старшинство
операций при вычислении логических выражений
Для логических выражений без скобок принят
следующий порядок вычислений:
- вычислить арифметические и строковые выражения
в отношениях, потом отношения
- вычислить логические функции
- вычислить операции отрицания
- вычислить операции логического умножения
- вычислить операции логического сложения
- порядок
действий может быть изменен при помощи круглых скобок
В лабораторном практикуме две работы 14.2 и
14.4 позволяют ознакомиться с геометрическими интерпретациями булевых функций,
описывающих событие "точка принадлежит области".
Булева
алгебра и ее интерпретации
Раздел математики, изучающий законы алгебры
двух значений, был впервые исследован Дж. Булем и потому эту алгебру часто
называют булевой алгеброй.
Алгебра - это множество чисел, замкнутое
относительно выбранного множества операций над ними. В булевой
алгебре операции И (умножение), ИЛИ (сложение), НЕ (отрицание) над числами из
{0,1} дают результат, попадающий в то же множество {0,1}.
Булева функция (БФ) - это двоичная
функция двоичных аргументов. Область определения булевой функции, зависящей от n
аргументов, - это 2n двоичных наборов значений аргументов.
Значения БФ на каждом из наборов образуют таблицу истинности БФ.
Таблица истинности для
f2(x,y)
Xy f2(x,y)
00
0
01
1
10
0
11
1
Буль показал, что любую сколь угодно сложную
логическую функцию можно записать, используя всего лишь три базовые логические
операции: сложение x+y, умножение xy и отрицание ~x.
Таблицы истинности 3 основных операций:
|
Xy сложение x+y
|
xy
умножение xy x*y x&y
|
x отрицание
~x
|
|
00
0+0=0
|
00
0*0=0
|
0 ~0=1
|
|
01 0+1=1
|
01
0*1=0
|
1
~1=0
|
|
10 1+0=1
|
10
1*0=0
|
|
|
11 1+1=1
|
11
1*1=1
|
|
Значения, которые принимают аргументы x и y
- это 0 либо 1. Результат выполнения любой операции - 0 либо 1. Старшинство
операций в булевой алгебре такое же как и в обычной алгебре:
1. отрицание или инверсное значение
2. умножение
3. сложение
Умножение полностью похоже на обычное
умножение. Сложение отличается от обычного только последней строкой - и тут
надо вспомнить, что результат должен быть в том же множестве чисел {0,1}.
Сравним с обычной алгеброй свойства 0 и 1 (отличие в последнем соотношении):
0*x = 0 0+x = x
1*x = x
1+ x = 1
Для логической величины x справедливо:
·
x + x = x проще приведение подобных
·
x x = x нет степеней
Для инверсной величины справедливо:
·
~(~x) = x - вспомните из обычной алгебры -(-x) =
x
·
x(~x)=0
·
~x + x = 1
Законы булевой алгебры. В обычной алгебре можно найти аналоги всем
перечисленным ниже законам булевой алгебры (кроме последнего дистрибутивного):
|
Коммутативность
|
Ассоциативность
|
Дистрибутивность
|
|
xy
= yx
|
x(yz)
= (xy)z
|
x(y+z) = xy + xz
|
|
x+ y
= y + x
|
x+(y+z) = (x+y)+z
|
x+(yz)
= (x+y) (x+z)
|
В булевой алгебре в отличие от обычной
алгебры справедлив принцип двойственности. Все законы
симметричны относительно умножения и сложения - заменив умножение на
сложение и наоборот сложение на умножение, получим также справедливый закон:
|
~(x+y) = ~x
|
~y ~(xy) = ~x + ~y
|
законы Деморгана
|
|
xy + x~y = x
|
(x+y) (x + ~y) = x
|
законы склеивания
|
|
xy + x = x
|
(x+y) x = x
|
законы поглощения
|
Общим методом доказательства справедливости
закона в булевой алгебре может служить метод
испытаний на тривиальном тесте из 2n наборов: левую и
правую часть тождества вычисляют на всех возможных значениях аргументов и
сравнивают на полное совпадение.
Пример: докажем закон склеивания
xy + x~y = x
|
Xy
|
xy
+ x~y
|
x
|
сравнение
|
|
00
|
00 +
0~0=0+0=0
|
0
|
равны
|
|
01
|
01+0~1=0+0=0
|
0
|
равны
|
|
10
|
10+1~0=0+1=1
|
1
|
равны
|
|
11
|
11+1~1=1+0=1
|
1
|
равны
|
Интерпретации булевой функции
Интерпретация булевой функции в какой-либо
предметной области предполагает, что можно придать некий смысл в
соответствующей терминологии
·
и двум значениям
·
и трем операциям
·
и шести отношениям
·
и вообще любым законам булевой алгебры
Например для двух значений возможны
интерпретации
·
0 либо 1
·
ИСТИНА либо ЛОЖЬ
·
TRUE либо FALSE
в Паскале
·
.TRUE. либо
.FALSE. в Фортране
·
0 либо не 0 в языке С
·
высокий уровень (5v) либо низкий уровень
напряжения (0v)
·
точка принадлежит либо не
принадлежит некоторой области
Чем примитивнее алгебра, тем больше у нее
приложений. Наиболее важными можно считать следующие интерпретации булевой
алгебры
·
математическая логика и основания
математики
·
исчисление высказываний
·
теория множеств
·
переключательные функции как раздел
теории автоматов
·
логические схемы компьютеров
·
геометрическая интерпретация
·
топологическая интерпретация
·
язык запросов в системах управления
базами данных
Привлекая образное мышление из смежной
интерпретации, легче вникнуть в смысл происходящего. Так, привлекая
геометрическую интерпретацию, можно легко понять новые алгебраические законы.
Например, закон 1+x=1 трудноват для новичка. Однако стоит вспомнить, что
"1"-это по принадлежности точек - вся плоскость. Тогда сразу понятно,
что объединяя всю плоскость с чем угодно, получим ее же.
Геометрическая интерпретация
булевой функции
Геометрическая интерпретация булевой функции
предполагает, что можно придать геометрический
смысл и двум значениям, и трем операциям, и шести отношениям, и вообще любым
законам булевой алгебры.
Два возможных значения будем
интерпретировать так
·
истина - как (.) точка принадлежит некоторой
области
·
ложь - как (.) точка не принадлежит
некоторой области
Функция принадлежности B(x,y) зависит от координат точки и
определяется через простейшие неравенства и логические операции. В крайних
случаях эта функция может быть константой, равной
·
B(x,y) = 0 (ложь)
для пустого множества
точек
·
B(x,y)=1 (истина) для всей плоскости
Отношения будем интерпретировать как
истина, когда
· 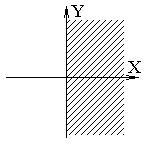
·
y>=0 - точка выше
0
·
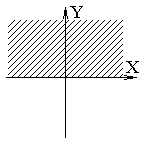 x2+y2>=1
- точка за кругом единичного радиуса
(на расстоянии 1 и более от цетра)
x2+y2>=1
- точка за кругом единичного радиуса
(на расстоянии 1 и более от цетра)

Отношения будем интерпретировать
как ложь, когда
·
.not. x>=0 или x<0 - точка не правее 0 (левее и в нуле)
·
.not. x>=0 или y<0 - точка не выше 0 (ниже и в
нуле)
·
.not.x2+y2>=1 или x2+y2<1 - точка
внутри круга
единичного радиуса (на расстоянии не более
1 от цетра)
Логические операции приобретают смысл
манипуляций со множествами точек, образующими некие области A (желтая), B (зеленая)
на плоскости.
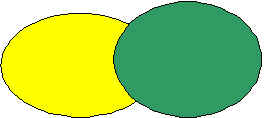
Логическое умножение - пересечение (красная-общая
часть) двух множеств точек
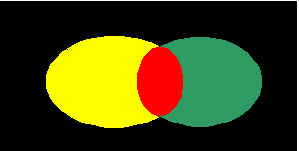
области
AB комбинация областей умножение AB входит ли в пересечение
00 вне x и вне у 0*0=0 нет
01 вне x и внутри у 0*1=0 нет
10 внутри x и вне у
1*0=0 нет
11 11 внутри x и внутри у 1*1=1 да
Логическое сложение –объединение двух множеств точек, объединение неисключающее.

области
AB комбинация областей
сложениеA+B входит ли в объединение
00 вне x и вне у 0+0=0 нет
01 вне x и внутри у 0+1=1 да
10 внутри x и вне у 1+0=1 да
11 внутриxивнутри у 1+1=1 да
Логическое
отрицание(инверсия) – дополнение множества
точек до всей плоскости,
например,
черная область"не в круге".
A - область
отрицание ~Ax то входит в дополнение
0 вне x ~0 =1
внутри A 1 внутри x~1=0
вне A
Пример 1 Квадранты и оси,
realx , y
Logical first, second, third, forth, p00, X_axes,
Y_axes,point_234
! когда отношения записаны в стиле Ф-77
p00 = x
.eq. 0 .and. y.eq. 0 ! начало координат
first = x.gt. 0 .and. y.gt.0 ! 1-ый квадрант
second = x .lt. 0 .and. y.gt.0 !2-ой квадрант
! когда отношения записаны в стиле Ф-90
third = x<0 .and. y<0 !
3-ий квадрант
forth = x>0 .and. y<0 !4-ый
квадрант
X_axes = y==
0 !
на оси X
Y_axes = x==
0 !
на оси Y
point_234
= second .or. third .or. forth ! 2,3,4-ый квадранты
point_234 = x .lt. 0 .or. y.lt.
0 ! 2,3,4-ый квадранты
point_234 = .not.
first .and. .not.X_axes .and. .not.Y_axes
Как видно из этого примера, одно и то же
высказывание point_234 может быть представлено в нескольких
эквивалентных формах, что соответствует эквивалентным преобразованиям
логической формулы по законам булевой алгебры.
Пример 2
Попадание точки (x,y) в верхний полукруг
единичного радиуса, отношения записаны в стиле Ф-90
realx , y; Logical point
point = y>=0 .and. 1<=y*y+x*x ! выше
оси X И внутри
круга
write(*,*)'для x=', x, 'и для y=', y, 'точка
в верхнем полукруге' , point
Топологическая интерпретация
булевой функции
Топология характеризует состав
геометрической фигуры путем разложения на составляющие.
Например, для функции 2 переменных f2(x,y)
область определения - это 4 набора.
В топологической
интерпретации - это вершины квадрата с единичной стороной
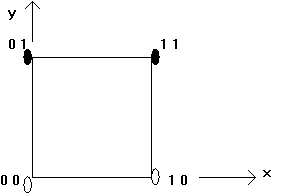
Черным закрашены вершины, где БФ равна “1”
Таблица истинности для f2(x,y)
Xy f2(x,y)
00 0
01 1
10 0
11 1
Для приведенной в таблице функции f2
·
каноническая форма f2 =~xy+xy
·
упрощенная форма f2=y
Для функции 3 переменных f3(x,y,z) область
определения - это 8 наборов.
В геометрической интерпретации - это вершины
куба с единичной стороной.
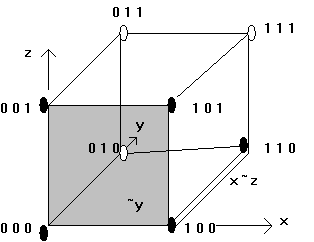
Черным цветом закрашены те вершины, где БФ равна “1”
Таблица истинности
Xyz F3(x,y,z)
000 1
001 1
010 0
011 0
100 1
101 1
110 1
111 0
Для приведенной в таблице функции F3
·
каноническая форма F3=~x~y~z+
~x~yz + x~y~z + x~yz + xy~z
·
упрощенная форма F3=~y + x~z
Унифицируя геометрическую терминологию, кубом называют
·
не только 3-мерный куб
·
но и 2-мерный квадрат
·
и одномерное ребро
·
и даже отдельную вершину
то есть все множество подмножеств точек -
элементы покрытия области определения БФ.
При большем числе измерений можно говорить и
о 4-мерном, 5-мерном кубе и т.д.
Когда наши геометрические представления
пасуют, сохраняя геометрическую терминологию, переходят, подобно аналитической
геометрии, к алгебраическим выкладкам. Например, комплекс подкубов 3-мерного
куба -
·
8 вершин {000, 001, 010, 011, 100, 101,
110, 111},
·
12 ребер {00x, x01, 10x, x00, 01x, x11, 11x,
x10, 0x0, 0x1, 1x1,1x0 },
·
6 граней {1xx, 0xx, x1x, x0x, xx1, xx0}
Из этого материала и собирают любую БФ 3
переменных. В кубе нулем"0"и единицей"1", указывают
неизменные координаты (0 указывается для термов с “~”), изменяющиеся координаты
указывают знаком"x". Примеры кубов 001, x0x, 1x0. Например,
единицы БФ F3(x,y,z), зависящей от трех переменных можно накрыть двум кубами
{x0x, 1x0}, что полностью соответствует упрощенной форме функции F3.
Доказано, что по таблице истинности можно
записать БФ в канонической форме – в виде суммы произведений. В
канонической форме столько слагаемых, сколько “1” в таблице истинности,
а каждое слагаемое - это произведение всех переменных, причем те
переменные, которые в строке таблице истинности равны “0”,берутся с инверсными
“~“.
Пример: по таблице истинности запишем
функцию f(x,y) в канонической форме f1:
xy
f(x,y)
00
0
01
1
первое слагаемое ~x y, так как в этом наборе x=0,
аy=1
10
0
11
1
второе слагаемое xy, так как в этом наборе x=1,
аy=1.
Каноническая форма f1- это сумма
указанных произведений f1=~xy+xy Аналогично для приведенной ранее
функции 3 переменных получим каноническую форму f1 в виде 5
слагаемых f1=~x ~y~z + ~x~yz + x~y~z + x~yz + xy~z
По законам булевой алгебры каноническую
форму можно упростить.
К примеру, по закону склеивания для f1 получимf1=~xy
+ xy = y. Преобразование функции 3 переменных более громоздко. Принимая во
внимание геометрические свойства можно, к счастью, предсказать результат
упрощения канонической формы, записав ожидаемый результат по покрытию “1”
на картинке.
Действовать надо так:
·
в первую очередь покройте, если
можно, закрашенные точки гранями- по 4 точки
·
затем ребрами- по 2 точки
·
и оставшиеся непокрытыми –вершинами
по 1 точке
После этого остается выписать упрощенную
форму: в нее войдет столько слагаемых, сколько потребовалось кубов в
покрытии (для рассматриваемой функции 3 переменных будет 2 слагаемых). Остается
записать каждое слагаемое как произведение значений переменных, постоянных в
пределах куба(если“1”-без инверсии, если “0” -с инверсией “~”).Обратите
внимание: не запрещается, чтоб ребро и грань имели общую вершину. Общее
правило: стремитесь покрыть одним кубом максимально возможное число закрашенных
вершин.
Посмотрим еще раз на картинку области
определения функции 3 переменных: на нем имеется 5закрашенных вершин, где F3(x,y,z)=1.
На перед ней грани находится 4 таких вершины и на этой граниy=0, а x
и z изменяются, что дает первое слагаемое y. На нижнем правом
ребре, покрывающем две закрашенные вершины (100) и (110), x=1 и z=0,
а y изменяется, что дает второе слагаемое x~z. Имея в виду
сказанное, получим, что предсказываемая упрощенная форма функции 3 переменных
такова: F3=~y+x~z для алгебраического упрощения потребуется неоднократно
применить законы склеивания и поглощения.
Как в обычной алгебре, можно проводить
преобразование формул по законам булевой алгебры.
В качестве примера преобразуем~F3(x,y,z),чтоб
получить упрощенную форму для~F3(x,y,z)
~F3(x,y,z) =~( ~y + x~z) =~ ~y(~(x~z)) = y(~x
+ ~~z) = y~x+ yz
где ~( ~y + x~z) =~~y(~(x~z)) ==> по
правилу Деморгана
~(x~z) = ~x + ~~z =
~x+z ==> по правилу
Деморгана
y(~x + z)= ~xy +
yz ==> дистрибутивный
закон
Нетрудно предсказать этот результат,
используя геометрическую интерпретацию инверсной функции~F3 (изменив на
противоположную раскраску вершин)
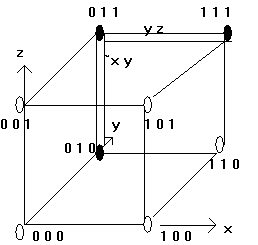
Черным закрашены вершины, где инверсная БФ равна “1”, а
исходная наоборот "0"
~F(x,y,z) = ~xy + yz
Таблица
истинности
xyz ~F3
000 0
001 0
010 1
011 1
100 0
101 0
110 0
111 1
Обработка строк –
строковые выражения
Строки представлены по-разному в разных языках
- в
Фортране - как строки фиксированной длины, когда длина строки (по
числу символов) указана в описании
- в
Паскале - как строки переменой длины, когда длина строки
прилагается к самой строке
- в С
- как строки неопределенной длины, когда длина строки явно не
указывается, а вместо этого в конце имеется так называемый 0-символ –
признак конца строки
Помимо обработки числовой информации в ФОРТРАНе-90 предусмотрена обработка
строк. При всем различии в истолковании арифметических и строковых выражений
подход к их определению и построению очень схож. Особенности строковых
выражений связаны с понятием "подстроки" и наличием единственной
операции над строками – операции сцепления, называемой также в
некоторых книгах конкатенация.
Строковые
константы, переменные и подстроки
Строковые константы, переменные и
подстроки иллюстрируются примером программы.
Пример 1: "угадай-ка мое имя с 3
раз" – см. таблицу ниже.
Как и для других типов данных различают явные и именованные константы:
·
явная строковая константа - это текст
·
либо заключенный в 'апострофы', см. 'ocenka.txt' на линии 6 – так задано имя файла в
операторе открытия файла
·
либо текст, заключенный в кавычки, см. линию 8, если в самом тексте
уже есть 'апострофы', как здесь 'Вася' в
тексте
"Как мое имя? Например, отвечай: 'Вася' "
- именованная
константа, например PCname, на линии 5, определяется обычным
образом character*6 , parameter :: PCname='IBM-PC'
- атрибут
character - описание типа
- атрибут
parameter – признак константы
- PCname='IBM-PC'
- имя PCname и значение константы 'IBM-PC'
|
Линия
|
Оператор
|
|
1
|
! про работу со строками
|
|
2
|
Program request
|
|
3
|
integer Point
|
|
4
|
character*6 name, mark *17
|
|
5
|
character*6 , parameter :: PCname='IBM-PC'
|
|
6
|
open(6,file='ocenka.txt')
|
|
7
|
Do Point = 1,7
|
|
8
|
Write(*,*) "Как мое имя? Например, отвечай: 'Вася' " !ASCII
|
|
9
|
read(*,*) name
|
|
10
|
If( name== PCname )
exit
|
|
11
|
Enddo
|
|
12
|
Select Case( Point ) ! Point
{1,2,3,4,5,6,7,8}
|
|
13
|
Case(1 )
|
|
14
|
mark = 'отлично'
|
|
15
|
Case( 2 )
|
|
16
|
mark = 'хорошо'
|
|
17
|
Case( 3 )
|
|
18
|
mark = 'удовлетворительно'
|
|
19
|
Case( 4 )
|
|
20
|
mark = 'плохо'
|
|
21
|
Case Default !
Point {5,6,7,8}
|
|
22
|
write(*,*) ' кол - думать надо? '
|
|
23
|
End Select ! .. Point
|
|
24
|
write(6,*)
'оценка ' , mark // ' - за ', Point, ' попыток'
|
|
25
|
End
|
Строковые величины - константы, переменные, функции относят к
базовому типу character. В операторе character
для каждой из строк указывается её длина, постоянная по числу
символов. Имеется некоторое разнообразие в указании длин:
- все
строки имеют одну и ту же постоянную длину, равную 1
character Symbol, strike
- все
строки имеют одну и ту же постоянную длину, в этом примере равную 6
character *6 name, PCname
·
длина описана константами индивидуально
character NATURE*17, Symbol*1
причем, если опросить длины строк, получим
len(NATURE)=17, len(Symbol)=1
·
сочетание разных способов задания длин строк, например для
character*6 name, PCname, mark *17 получим
len(name)=len(PCname)=6,
len(mark)=17
·
длина строки может быть задана константным выражением,
заключенным в скобки, например integer, parameter :: c=6;
character* (2*с+1) string
в примере c-целая константа, 2*с+1 – целое константное выражение, len(string
)=13
·
длина строки string
может быть задана (*) , если эта строка является параметром
подпрограммы, в этом случае
·
длина строки указывается в вызывающей программе
·
в подпрограмме len(string ) – это неизменная величина, но, быть может, разная для
разных вызовов подпрограммы, как в примере
program glavn
character
nature*17,
Symbol*1
call podprogr (nature) ! увидим len(string )=17
call podprogr (Symbol) ! увидим len(string )=1
end program glavn
subroutine podprogr(string )
character(*), intent(in) :: string
write(*,*) ‘len(string )=’,
len(string )
end subroutine podprogr
Символы в строке string нумеруются слева направо,
начиная с 1 до Len(string ).
|
1
|
2
|
p .. ..
|
q
|
Len(string )
|
|
string (1:1)
|
string (2:2)
|
|
|
string (Len(string
) : Len(string ))
|
|
|
|
подстрока
string (p:q)
|
|
Чтобы указать подстроку пишут string (p:q),где 1<=p<= q<=Len(string
), p и q целые константы, переменные или арифметические выражения.
Дадим некоторые разъяснения относительно написания подстрок
·
при p=1 допускается писать string (:q)
·
при q=Len(string) допускается
писать string (p:)
·
string (:) – это всё равно, что
просто string
·
string (p:q) – это пустая строка,
если p>q
·
аварийное сообщение "subsript out of range" при
выполнении программы будет говорить о выходе индекса p или q за
границы строки [1, Len(string ) ]
Стандартные функции обработки строк
Перечислим основные функции:
·
L=Len (string) - длина строки -
определена, даже если string еще и не вычислена
·
N = Len_trim(string ) - длина строки
без хвостовых пробелов; после N-ого символа в строке string
только пробелы
·
npos = Index( string, substring
[, back]) - найти вхождение подстроки substring в строку string
·
аргументами функции являются
·
строка string,
·
подстрока substring,
·
необязательный back - направление поиска
·
результат - номер символа в строке string, где начинается вхождение substring в строку string, считая, что символы всегда нумеруются слева
направо
·
npos =0, если не найдено вхождение подстроки substring в строку string
·
необязательный параметр logical back указывает, в каком направлении ищется первое вхождение
подстроки
·
если back отсутствует или back=.false. - ищется слева
направо
·
если back присутствует и back=.true. - ищется справа налево
·
например
·
npos =Index(‘абракадабра’, ’бра’)
даст npos = npos 2
·
npos =Index(‘абракадабра’, ’бра’, .true. )
даст npos =9
·
npos =Index(‘абракадабра’, ’Бра’)
даст npos =0, так как символы ’Б’ и ’б’ имеют
разные коды
·
npos =Index(‘абракадабра’, ’добра’)
даст npos =0, так как ’добра’ нет
·
code = ichar( Symbol ) - определить код code отдельного
символа
character
*1 Symbol;
code = ichar( Symbol )
· Symbol =char(
code ) - определить символ по заданному коду, то есть
функция, обратная к ichar
·
trim(string ) - отбросить хвостовые пробелы
- функция имеет смысл как часть строкового выражения
·
npos = scan ( string, characters [, back] )
найти вхождение одного из символов строки characters в строку string
·
результат - номер любого символа из characters в строке string, при нумерации с 1 слева направо
·
аргументами функции являются строка string и
строка characters
·
npos =0, если символов строки characters в строке string нет
· пример поиска первой позиции любой
цифры в строке string
character*80
string; integer npos
npos= scan(string,'1234567890' )
·
необязательный параметр logical back указывает, в
каком направлении ищется первое вхождение одного из символов строки characters
·
если back отсутствует или back=.false. - ищется слева направо
·
если back присутствует и back=.true. - ищется справа налево
§
при том, что нумерация позиций в string всегда с 1 и слева направо
Строковое выражение и строковый оператор присваивания
Строковое выражение строится только из величин типа character
·
строковых констант
·
строковых переменных
·
строковых функций, стандартных или своих
·
подстрок
·
с применением единственной операции a//b , называемой
·
сцепление строк
·
или по-другому конкатенация строк
Вычислив строковое выражение, получим строку.
Под сцеплением a//b понимается строка, в которой за символами строки
a следуют символы строки b.
Понятно, что Len(a//b)=Len(a)+Len(b),
причем Len(a//b)>Len(a)
и Len(a//b)>Len(b).
Например, чтобы устранить лишние пробелы в
"хвосте" словесной оценки.
Вместо линии 24 можно было бы написать так
write(*,*) 'оценка ' , mark( 1:Len_trim(mark))
// ' - за ', 6-Point, ' попыток'
хотя лучше write(*,*) 'оценка ' , trim(mark)
// ' - за ', 6-Point, ' попыток'
Строковый оператор присваивания имеет обычный вид string =e
·
где string - строковая переменная, e –строковое
выражение
·
при len(e)=len(string )
результат e заносят в string без изменения
·
при len(e )>len(string )
результат e "усекается" справа по длине строки string
string = e(1:Len(string ) )
·
при Len(e)<Len(string ) результат e дополняется справа
пробелами недостающими до длины len(string)
Подстроки одной и той же строки слева и справа от знака присваивания
"=" не должны иметь общих элементов:
character nature*17
NATURE(3:6) = NATURE(5:7) ! с ошибкой (5-ый и 6-ой символ - общие)
Пример. Опробелить строку str. character str*10
str = ' '. В константе ' ' не обязательно указывать 10 пробелов, так как
дополнение пробелами произойдет автоматически по длине строки str.
Заключительные замечания и примеры
Обратите внимание
·
строковый оператор присваивания string=string//’s’ не имеет смысла в
Фортране, хотя и является аналогом популярного оператора присваивания k = k
+1; объяснение в фиксированной длине строки string :
·
сначала string//’s’ удлиняет длину строки на 1,
·
затем присваивание “=” обрезает результат string//’s’ по длине string
·
таким образом string вообще не изменяется, делая string=string//’s’ бессмысленным
·
вообще string3 =
string1// string2 бессмысленно, если len( string1)= len(
string3)
·
сначала string1// string2 даёт длину строки len( string1)+ len( string2),
·
затем присваивание “=” обрезает результат string1// string2 по длине string3
·
таким образом, string3 вообще не изменяется, делая string3 = string1// string2 бессмысленным
·
как правило, имеет смысл писать
string3 = trim(string1)// string2, а не string3 =
string1// string2,
·
чтоб внутрь string3
не попадали хвостовые пробелы string1
·
чтоб строка string1//
string2 не
стала длиннее строки string3
·
в string3
= trim(string1)// ‘длинную текстовую константу нельзя
прерывать концом строки’
чтоб не получить пробелы в месте разрыва, а правильно переносить так
string3 = trim(string1)// ‘длинную текстовую константу’//
’ нельзя прерывать концом строки, но можно сцеплением’
Следует помнить, что при вводе/выводе строк
· вводимую строку
заключают в апострофы для ввода/вывода под управлением списка
(в скобках read второй параметр – это “*”)
так при использовании read(1,*) список_ввода
'вводимая_строка_в_апострофах' – должна быть подготовлена в файле
· вводимую строку заключают
в апострофы для поименного ввода/вывода
так при использовании
character*17 stroka; Namelist /имя_списка/список
переменных, в том числе stroka; read(1,имя_списка)
.. , stroka='вводимая_строка_в_апострофах', .. – должна быть подготовлена в
файле
· строку не
заключают в апострофы только для форматного ввода/вывода с
использованием read(1,32); 32 format(a)
вводимая_строка_без_апострофов в файле
Кодовые таблицы
Относительно применения кодовых таблиц следует
обратить внимание на то, что
· кодовая таблица ANSI для
английского, русского алфавита и других символов доступна в помощи FPS 4. 0
· кодовая таблица ASCII
для английского, русского алфавита и других символов доступна в редакторе ME
по Alt^A.
· разглядывая эти
таблицы можно отметить:
· строгое упорядочение
по кодам символов английского алфавита, цифр, пробела
·
ichar("пробел")< ichar('0')
..< ichar('9')< ichar('A') ..< ichar('
Z') ..< ichar('a') ..< ichar('z')
· кодирование" вразброс"
для русского алфавита, что иногда вызывает затруднения при сравнении строк с
русскими буквами
· строки считаются
упорядоченными по алфавиту (точнее - по кодовым таблицам), как в словаре. Все
отношения, применяющиеся для чисел, доступны и для строк - в линии 11 примера 1
строки сравниваются на равенство
Следует иметь в виду, что
неправильно расхожее мнение, будто
·
русский в Windows
не работает
·
русский в Fortran не работает и т.д.
Объясняется подобное явление
определенным недопониманием. Относительно разных кодовых таблиц надо
понимать
- в DOS была
одна кодовая таблица ASCII
- разработчиками
Windows предусмотрено сосуществование двух, а не одной
кодовых таблиц
· write(1, *) для
файлов используется новая кодовая таблица ANSI из Windows
· write(*, *) - для
консоли используется старая таблица ASCII из DOS
· к сожалению, эти
таблицы не совпадают в русской части алфавита
· в английской части
алфавита, эти таблицы совпадают
· английский текст правильно
выглядит всегда, в том числе на консоли, как бы его не набирали
· чтобы русский текст правильно
выглядел на консоли надо его набрать
· в DOS-программе, например, vc , nc –
Волков или Norton-commander
· в Windows-приложении, поддерживающем обе
кодировки, например far
· использовать функции
языка С, которые обеспечивают перекодирование “на лету”, например
· CharToOem для
перехода из ANSI в ASCII
· OemToChar для
перехода из ASCII в ANSI
потребуется явный интерфейс, например для OemToChar
interface
subroutine OemToChar(int1_name,AnsiName)
!MS$ATTRIBUTES ALIAS:'_OemToCharA@8' :: OemToChar
integer*1 int1_name(81) !
буфер ASCII
С -подобной строки с 0-символом
integer*1 AnsiName(81) ! буфер ANSI С -подобной строки с
0-символом
end subroutine OemToChar
end interface
Заключительные примеры на обработку строк
Пример 2. Замените русское вопросительное предложение на
повествовательное предложение.
character*80 :: string=’Хорошо?’; integer stringPos
open(6,file='ocenka.txt')
write(6,*) ‘вопросительное предложение: ’,string
stringPos= index(string,’?’)
!
ищем позицию ’?’
if ( stringPos >0 ) then
string(stringPos : stringPos)=’.’ ! если нашли – заменяем ’?’ на ’.’
write(6,*)
‘повествовательное предложение: ’,string
else ! если не нашли
write(6,*) ‘нет вопросительного
предложения ’
endif
end
Пример 3. Имеется текст на английском языке. В нём несколько
предложений. Среди них имеется единственное вопросительное предложение,
начинающееся со слов “Do you.. “. К прежнему тексту добавьте повествовательное
предложение, переделанное из вопросительного предложения по схеме “I .. too.“: с - I начинается
– заканчивается too.
Например:
How do you do. Do you speak English? I speak English.
превратить в
How do you do. Do you speak English? I speak English. - I speak English too.
|
1
|
DoyouPos=16
|
znakPos =36
|
Len(string )=180
|
|
1
2
3 4
5
1234567890123456789012345678901234567890123456789012345567890
|
|
How do you do. Do you speak English? I speak
English.
|
|
How do you do. Do you speak English? I speak
English. - I speak English too.
|
character*180 :: string=’
How do you do. Do you speak English? I speak English.’
integer DoyouPos, znakPos
DoyouPos = index(string,’ Do you’) ! ищем начало предложения по фразе ’ Do you’
znakPos = index(string, ‘ ?’) ! ищем
конец предложения по ‘ ?’
if( DoyouPos>0 .and. znakPos>0) write(6,*)trim(string)//'
- I' // string(DoyouPos +7: znakPos -1) // '
too. '
Обратите внимание на то, что при формировании новой строки
·
проверяется, что нашли, что хотели найти
·
новая строка составлена из четырёх частей
o
из старой строки при помощи функции trim отброшены хвостовые пробелы
o
константа ' - I'
o
string(DoyouPos +7:
znakPos -1)
– часть старой строки без ’ Do you’
o
константа ' too. '
Пример 4. Классифицируйте вводимые предложения по типу:
без пунктуации, повествовательное, вопросительное, восклицательное, с
многоточием…
Program proga4
character text*80, znak*1
character*3, parameter :: znaki = '!?.'
integer textPos, znakPos
write(*,*) 'string=?'; read(*,*) text
textPos = scan(text, znaki); ! ищем позицию !?. в тексте
if(textPos ==0 ) stop 'no punctuation' ! знаков !?. не нашли в тексте
znak = text (textPos: textPos); ! нашли и выбираем знак по позиции в тексте
znakPos = index (znaki, znak) ! ищем позицию знака в строке '!?.'
select case(znakPos) ! разбор случаев, каким бы мог оказаться знак
case
(1); write(*,*) 'vosklicat!'
case (2); write(*,*) 'voprosit?'
case (3)
if(text (textPos: textPos +2) =='...')write(*,*)
'nezavershen...' ! с многоточием…
if( len_trim(text)== textPos) write(*,*)
'povestvovat.' ! точка-последняя в строке
end select
end Program proga4
Оператор
присваивания
Оператор присваивания
переменная = выражение
позволяет сохранить в переменной значение,
вычисленное по формуле, в данном случае знак "=" используется не
как знак тождества, а как знак присваивания.
Имеется три разновидности оператора присваивания
·
арифметический оператор присваивания
Числовая_переменная = арифметическое_выражение
·
логический оператор присваивания
логическая_переменная = логическое_выражение
·
строковый оператор присваивания
строковая_переменная = строковое_выражение
Относительно выражения справа от "=" и переменной слева
от "=" в логическом операторе присваивания действуют следующие
правила
·
оба должны быть одного и того же логического типа logical, но могут
иметь не одинаковые разновидности logical*4 logical*2 logical*1
·
сначала вычисляется логическое выражение
·
в случае одинаковых разновидностей результат вычисления выражения будет
сразу присвоен переменной слева от "="
·
в случае не одинаковых разновидностей (разнятся по числу байтов) до
присваивания изменяется форма представления результата по числу байтов в ПК
·
потом результат присваивается переменной
Относительно строкового выражения справа от "=" и
переменной слева от "=" в строковом операторе присваивания действуют следующие
правила
·
оба должны быть одного и того же строкового типа
character,
но могут иметь не одинаковую длину строки, указанную в character * длина , заметим, что просто character подразумевает длину строки равную 1
·
сначала вычисляется строковое выражение
·
в случае одинаковых длин строк результат вычисления выражения будет
сразу присвоен переменной слева от "="
·
в случае не одинаковых длин строк (разнятся по числу символов-байтов) до
присваивания изменяется длина строки результата по числу байтов на длину строки
переменной
·
результат справа усекается, если результат длиннее переменной
·
результат справа дополняется пробелами, если результат короче
переменной
·
потом результат присваивается переменной
Относительно выражения справа от "=" и переменной слева
от "=" в наиболее сложном арифметическом
операторе присваивания действуют следующие правила
·
обязательно оба они должны быть числового типа из integer, real, complex
·
не обязательно оба они должны быть одного и того же типа и одной и
той же разновидности
·
сначала вычисляется арифметическое
выражение справа от "=" с автоматическим определением типа
выражения и всех его подвыражений
·
в случае одинаковых типов и одинаковых
разновидностей у обоих результат вычисления выражения будет сразу присвоен
переменной слева от знака "="
·
в случае разных типов до присваивания
тип результата вычисления арифметического выражения будет
преобразован к типу числовой переменной
·
в случае одинаковых типов, но не одинаковых
разновидностей (разнятся по числу байтов) до присваивания изменяется форма
представления числа в компьютере по числу байтов
·
при переходе в более узкий класс чисел
производится так называемое усечение, например, если k-целая, то дробная
часть вычисленного вещественного выражения просто отбрасывается
так для k = 12.8 - 5.0 получаем 12.8 - 5.0 =>
7.8 => 7 => k =7
·
заметим, что переход в более узкий класс
чисел может сопровождаться потерей информации, выходом за диапазон представимых
в компьютере чисел (переполнением)
Тип может быть преобразован целенаправленно
с помощью исчерпывающего набора стандартных функций преобразования типа
·
например, функция int(x) преобразует x любого
числового типа в целое число integer*4
·
например, функция real(x) преобразует x любого
числового типа в вещественное число real*4
·
прочие – см. в помощи FPS 4.0
Диапазоны чисел, представимых в ПК IBM-PC, и
разновидности типов таковы
o
для Integer - целых чисел имеются
3 разновидности Integer*4, Integer*2 и Integer*1
o
стандартный Integer – это
для ПК то же, что Integer*4 [-1010,1010],
o
Integer*2 и Integer*1 имеют более узкий
диапазон, чем стандартный тип
o
работа с целыми числами точная
o
для Real - вещественных
чисел имеются 2 разновидности Real*4
и Real*8
o
стандартный Real – это для
ПК то же, что Real*4 [-1038,1038]
o
double precision - двойная точность – это
для ПК тоже, что и Real*8 с более широким диапазоном [-10308,10308],
чем стандартный тип Real
o
работа с вещественными числами неточная
o
все числа вблизи 0.0 неразличимы с ним
o
аналогично неразличимы вещественные
числа вблизи заданного числа, справка об интервале неразличимости с использование
функции Epsilon(Real)
o
для Complex –
комплексных чисел имеются 2 разновидности Complex *16
и Complex *8,
причём последняя эквивалентна для ПК просто Complex
o
работа с комплексными числами неточная
o
для logical – логических
величин имеются 3
разновидности logical*1 logical*2 logical*4, причём
последняя эквивалентна для ПК просто logical
o
для character – строк
в ПК допустимы длины от 0 до 32767, причём character*1 эквивалентно
просто character
В языке "C" тот же знак
присваивания, что и в Фортране, а в Паскале в качестве знака присваивания
используется составной знак "
:= ".
Для сравнения двух величин в Фортране-90 и
"C" используется не привычный для математика знак " =
", а составной знак " == ". В Фортране-77 - знак сравнения
записывался как .EQ.
При написании сложной формулы рекомендуется
использовать промежуточные переменные, особенно полезные, если
какая-либо подформула повторяется многократно: в этом случае одновременно
упрощается запись формулы и сокращается число необходимых команд.
Обратите внимание,
·
(a+b)*(a-b) = a**2 – b**2 в Фортране никакого смысла не
имеет, а в математике тождество (a+b)(a-b) = a2 – b2
справедливо
·
популярный оператор присваивания K = K +1, увеличивающий значение
K на 1, как тождество не имеет смысла в математике
·
строковый оператор присваивания string=string//’s’ не имеет смысла в
Фортране, хотя и является аналогом популярного оператора присваивания k = k
+1; объяснение в фиксированной длине строки string :
·
сначала string//’s’ удлиняет длину строки на 1,
·
затем присваивание “=” обрезает результат string//’s’ по длине string
·
таким образом string вообще не изменяется, делая string=string//’s’ бессмысленным