|
|
 |
|
|
|
Вычисление функции
Вычисление функций разложением в
степенной ряд
Вычислением функций, а также многими
другими вопросами вычислений занимается раздел
математики, который называют по-разному
- вычислительная математика
- прикладная математика
- численные методы
- численный анализ
Задачи, которые здесь решаются
- сведение вычислений к простейшим операциям
- упрощение вычислений
- уменьшение числа операций и времени расчета
- уменьшение погрешности вычислений
В комплект Фортрана входят
тригонометрические функции, обратные
тригонометрические функции, экспонента,
логарифм. Мы используем их, не задумываясь о том,
как они вычисляются в компьютере. Однако
непосредственно в “железе” реализуются лишь
арифметические операции “ + - * / ”. Поэтому кто-то
в свое время должен был свести вычисление
функций к простейшим операциям и
запрограммировать стандартные функции. Часто
функции реализуют в виде степенных рядов. Все
перечисленные выше задачи возникают и при
суммировании степенных рядов. Упрощение
вычислений, уменьшение числа операций и времени
расчета, а также уменьшение погрешности
вычислений достигается применением рекуррентных
формул.
Пример sinx
Рассмотрим вычисление функции sinx.
Ряд Тейлора для этой функции имеет следующий вид
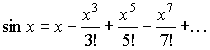
Ряд Тейлора является бесконечным
рядом, поэтому необходимо ограничить количество
его членов, входящих в сумму. Для сходящегося
ряда предел 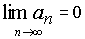 ,
следовательно, условие ,
следовательно, условие 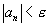 для любого положительного e
станет истинным, начиная с некоторого n. Сумма
бесконечного ряда ограничивается суммированием
первых n членов ряда, от a0 a1 до an-1.
Методическая погрешность оценивается по первым
отбошенным членам ряда для любого положительного e
станет истинным, начиная с некоторого n. Сумма
бесконечного ряда ограничивается суммированием
первых n членов ряда, от a0 a1 до an-1.
Методическая погрешность оценивается по первым
отбошенным членам ряда
- как |an| для знакопостоянного ряда
- как |an - an-1| для знакопеременного
ряда
где an первый отброшенный член
ряда.
Отметим, что помимо методической
погрешности на общую погрешность вычислений,
влияет постоянно накапливающаяся погрешность
округления. Погрешность округления – это
инструментальная погрешность, связанная с
ошибками процессора при работе с вещественными
числами.
При суммировании ряда по мере
возрастания n соперничают две встречные
тенденции
- убывает методическая погрешность
- накапливается и возрастает погрешность
округления
что создает для общей суммарной
погрешности вычислений характерную тенденцию с
минимумом. На падающем участке до минимума рост
затрат времени на вычисления оправдан
сокращением общей погрешности вычислений. В то
время как на последующем возрастающем участке
рост затрат времени ничем не оправдан, так как
суммарная погрешность вычислений растет.
Упрощение вычислений, уменьшение
числа операций и времени расчета, а также
уменьшение погрешности вычислений достигается
применением рекуррентных формул.
Ряд Тейлора для функции sinx можно
переписать в виде доступных “железу” команд
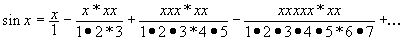
a0 a1 a2 a3 ...
Вычисления проходят слева направо.
Приглядевшись к
T0
T1 T2 ...
Tn-1
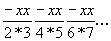 
можно заметить, что в каждом
последующем члене ряда меняется знак, а также в
числителе, и в знаменателе добавляется по два
сомножителя. Нетрудно понять каким будет
множитель Tn, на который надо домножить
предыдущий член ряда,
чтобы получить очередной член ряда a1
a2 a3 ... an
Именно такая формула an+1=an
Tn называется рекуррентной
формулой – она позволяет вычислить величину
очередного члена ряда, используя величину
предыдущего. Если обозначить последовательно
вычисляемые слагаемые как a0, a1,
a2, ..., то формула для вычисления
любого члена ряда примет вид:
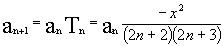
Продолжив рассмотрение вычисления
функции sinx, получим ту же рекуррентную
формулу аналитически. Ряд Тейлора для этой
функции имеет следующий вид
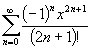 где где 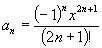 , n = 0, 1, 2, ... , n = 0, 1, 2, ...
Величину n! называют “n-факториал” и
записывают
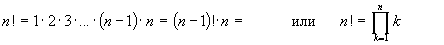
Принято считать, что 0!=1
Из формулы общего члена ряда следует,
что a0=x при n=0. Теперь каждый
следующий член ряда an+1 можно вычислить
с использованием уже вычисленного an с
помощью соотношения an+1 = an Tn, где n=0,1,2,…Сомножитель
Tn можно вывести из формулы 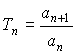
Выполним подстановки [ an+1
получен из an заменой n
на (n+1) ]
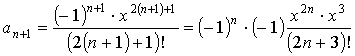
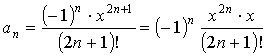
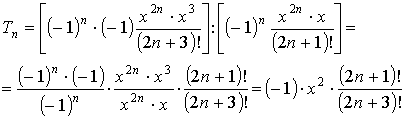
Чтобы сократить факториалы,
рассмотрим отдельно числитель и знаменатель. По
определению факториала
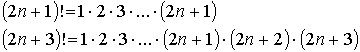
Сократив факториалы на (2т+1)! ,
окончательно получим тот же результат, что ранее
интуитивно
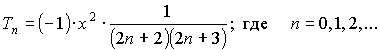
Отметим, что в полученном выражении
один из сомножителей, а именно –x2, не
зависит от n.
Проверка осуществляется применением рекуррентной
формулы
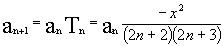
для получения
Задание
Составить программу, которая для
каждого значения аргумента x от начального значения
xo до конечного xk с шагом ?x :
- вычисляет значения функции f(x) по
стандартной программе;
- вычисляет приближенное значение функции с
помощью разложения в степенной ряд и определяет n
- число членов ряда, необходимое для получения
этого значения с заданной степенью точности для
заданного значения аргумента X
- печатает для каждого значения аргумента
- значение функции, вычисленное по стандартной
программе
- приближенное значение функции
- "точное" значение функции, вычисленное по
стандартной программе
- число членов ряда, необходимое для достижения
заданной степени точности
- разницу между приближенным значением функции и
"точным" значением функции
- границы и шаг изменения аргумента и значение
точности вычислений ввести с клавиатуры.
Результаты оформить в виде таблицы
- вычислить сумму ряда с низкой и высокой
степенью точности (например, 10-3 и 10-7
для синуса, который принимает значения из
интервала [-1,+1]), сравнить таблицы результатов
- с помощью пакета aGRAPHER показать 3 графика, а
именно:
- зависимость значения члена ряда от его номера
для выбранного значения x и его стемление к 0
- зависимость значения суммы ряда от ее номера и
его стемление к f(X)
- фиксированное значение f(X) для фиксированного
значения X
- подобрать X и точность так, чтоб число точек было
не менее 5
Программу следует создавать не по
образцу из методички (это конечная и недостижимая
цель, если действовать напролом), а
последовательным усложненим задачи
Var1. Задать в программе фиксированный
x (из допустимого диапазона) и фиксированную
степень точности,например, eps=0.001 (низкая для
синуса) и использовать простейший вывод
зависимости An-членов ряда от n–номера члена
ряда. Вычислить приближенное значение функции,
используя выведенную рекуррентную формулу для
членов ряда, и проконтролировать n - число
членов ряда, необходимое для получения этого
значения с заданной степенью точности. N не
должно превышать, например, 50. Программа содержит
лишь один цикл по возрастающим значениям n. С
помощью пакета GRAPHER рассмотреть зависимость
члена ряда от его номера n. По абсолютной
величине члены ряда должны непременно убывать.
Во избежание зацикливания программы
целесообразно установить некоторый верхний
предел Ndop для величины n. Если в процессе
вычислений значение n достигло значения
предела, то следует проверить:
- нет ли ошибки в формулах
- допустим ли X, сходится ли ряд
- разумна ли абсолютная погрешность, - сравни
дипазон возможных значений функции
- соизмеримы ли значения функции со
способностями компьютера по представлению чисел
- соизмерима ли погрешность со способностями
компьютера по представлению чисел
- нет ли ошибки в алгоритме или программе
- если ошибок нет, то можно попробовать увеличить
размер предела
- Var2.
Границы и шаг изменения аргумента x, а
также степень точности вычислений ввести с
клавиатуры. Не заботясь о красоте оформления
таблицы, сформировать колонки чисел для нее.
Строки таблицы формируются в цикле по аргументу x.
В строке представить аргумент x, точное
значение функции F(x), приближенное значение
функции как суммы ряда, модуль разницы между
вычисленной суммой по программе из Шага 1 и точным
значением функции F(x), число членов ряда n,
необходимое для обеспечения заданной степени
точности. Программа содержит цикл по
возрастающему n, вложенный в цикл по x.
Добиться, чтобы разница не превышала eps.
Возможно, что для знакопеременного ряда
потребуется именно такое условие окончания
суммирования (на шаге 1).
- Var3.
Теперь можно заняться форматированием
таблицы. Здесь тоже надо начинать не с заголовка,
а с внутренней строки таблицы. Прочитав
внимательно условие задачи, поняв диапазон
выводимых величин, можно прописать форматы
вещественных и целых полей. Эту внутреннюю
строку можно плавно переделать в FORMAT, заказав
оформление числовых полей, после чего заключить
числа между вертикальные разделители типа "
| : * I". Затем под внутреннюю строку можно
подогнать донышко и шапку таблицы.
- Следует пользоваться возможностями текстового
редактора ME или текстового редактора,
встроенного в оболочку MSDev-Fortran, работая с
несколькими окнами.
- В отчете представить:
- исходную формулу разложения функции в
степенной ряд
- рекуррентную формулу и вывод коэффициента
рекурсии
- проверку рекуррентной формулы
- блок-схему программы
- распечатки текста программы 1, 3
- таблицы с результатами вычислений с разной
степенью точности
- график обязательно представить на экране (в
дополнение можно и в виде распечатки)
Блок-схема программы
сравни в
методичке для варианта 3 |
| для варианта 1 -
оформляется самостоятельно |
Программа
Program Sin_var1 ! суммирование ряда
Implicit None
Real :: x=2.5 ! фиксированный допустимый
аргумент
Real :: eps=0.001 ! методическая погрешность
Integer :: n, Ndop=50 ! номер члена ряда и его MAX
допустимое значение
Real An,sum,f ! член ряда, сумма, функция
Namelist /avaria/ x,An, sum,f, eps, N, Ndop
Open(1,file="Teilor.txt") ! для просмотра
Open(2,file="An.txt") ! для aGRAPHER'a
An(n)
Open(3,file="sum.txt") ! для aGRAPHER'a sum(n)
Open(4,file="f.txt") ! для
aGRAPHER'a f(n)=const
Write(1,*) 'eps=',eps
n=0; An=x; sum=An ! стартовые значения n, A0 и суммы
ряда
f=sin(x) ! эталон по стандартной программе
Write(2,*) 0,An ; Write(3,*) 0,sum ; Write(4,*) 0,f ! начнем с n=0
для3 графиков
do while( Abs(f-sum)>eps ) ! суммируем,
пока сумма не сблизится с функцией
An = -An*x*x / ( (2*n+2)*(2*n+3) ); sum = sum+An; n=n+1
Write(2,*) n,An ; Write(3,*) n,sum; Write(4,*) n,f ! 3
графика=>agraher
if(
n>Ndop ) then ! проблемы в eps n An sum f-sum Ndop
Write(1, avaria); Stop " KARAUL!!!"
endIf
enddo
Write(1,*) x, f,sum, abs(f-sum), n ! окончательно
End
После выполнения программы в aGrapher
построены графики

Кроме того в текстовом файле Teilor.txt приведены числа
eps= 1.000000E-04
2.5 0.5984721 0.5984728 6.556511E-07 6
x, f,
sum, abs(f-sum),
n
Program Sin_var2 ! сперва
некрасивая таблица: x,f,sum,n,abs(f-sum)
Implicit None
Real:: x, Xn=-1.6,Xk=1.6,Xshag=0.2 ! аргумент, границы и шаг
его изменения
Integer :: n, Ndop=50 ! номер члена ряда и его MAX
значение
Real An,sum,f ! член ряда, сумма, функция
Real ::eps=0.001 ! методическая погрешность
Namelist /avaria/ x,An,sum,f, eps, N, Ndop
Open(1,file="Teilor.txt")
! для
просмотра
Write(1,*) eps
Do x = Xn, Xk+Xshag/2, Xshag
n=0; f=sin(x); An=x; sum=An ! старт n,A0 и суммы ряда
do while(
Abs(f-sum)>eps ) ! суммирование
ряда
An = -An*x*x / (
(2*n+2)*(2*n+3) ); sum = sum+An; n=n+1
if(
n>Ndop ) then ! проблемы в eps n An sum f-sum Ndop
Write(1, avaria); Stop " KARAUL!!!"
endIf
enddo
Write(1,*)x,f,sum,n,abs(f-sum) ! вывод строки
таблицы
EndDo
End
Program Sin_var3 ! красивая
таблица
Implicit None
Real:: x ! аргумент
Real:: Xn=-1.6,Xk=1.6,Xshag=0.2 ! границы и шаг
изменения X
Integer:: N, Ndop=50 ! номер члена ряда и его MAX
значение
Real An,sum,f ! член ряда, сумма, функция
Real:: eps=0.001 ! методическая
погрешность
Open(1,file="Teilor.txt") ! для
просмотра
Write(1,10)
eps! вывод ”шапки” таблицы
Do x = Xn, Xk+Xshag/2, Xshag
n=0; f=sin(x); An=x; sum=An ! старт n,A0, сумма ряда
do while(
Abs(f-sum)>eps ) ! суммирование ряда
An = -An*x*x / (
(2*n+2)*(2*n+3) ); sum = sum+An; n=n+1
if( n>Ndop ) then ! проблемы в eps n An sum f-sum Ndop
Write(1, avaria); Stop "
KARAUL!!!"
endIf
endDo
Write(1,12)x,f,sum,n,abs(f-sum) ! вывод строки таблицы
EndDo
Write(1,11) ! вывод ”донышка” таблицы
10 Format('методическая погрешность',E8.1
/&
’|--------|-------|-------|-----------|-----------|’/ &
’| x | станд |Тейлор.|Членов ряда| Разница |’/
&
’+-------+-------+-------+------------|-----------|’)
12 Format(’|’,F5.2,2(’|’,F12.7),’|’,I6,5x,’|’,e11.1’|’)
11 Format( &
’|-------+-------+-------+-----------+------------|’)
End
|
. |
|
|